|
|
|
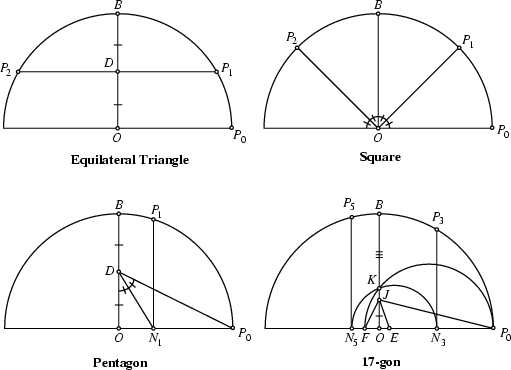
Compass and Straightedge constructions dating back to Euclid ![]() were capable of inscribing regular
polygons of 3, 4, 5, 6, 8, 10, 12, 16, 20, 24, 32, 40, 48, 64, ..., sides. However, this listing is not a complete
enumeration of ``constructible'' polygons. A regular
were capable of inscribing regular
polygons of 3, 4, 5, 6, 8, 10, 12, 16, 20, 24, 32, 40, 48, 64, ..., sides. However, this listing is not a complete
enumeration of ``constructible'' polygons. A regular ![]() -gon (
-gon (![]() ) can be constructed by Straightedge and
Compass Iff
) can be constructed by Straightedge and
Compass Iff
See also Compass, Constructible Number, Geometric Construction, Geometrography, Heptadecagon, Hexagon, Octagon, Pentagon, Polygon, Square, Straightedge, Triangle
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 94-96, 1987.
Courant, R. and Robbins, H. What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford, England: Oxford University Press, p. 119, 1996.
De Temple, D. W. ``Carlyle Circles and the Lemoine Simplicity of Polygonal Constructions.'' Amer. Math. Monthly
98, 97-108, 1991.
Dixon, R. ``Compass Drawings.'' Ch. 1 in Mathographics. New York: Dover, pp. 1-78, 1991.
Gauss, C. F. §365 and 366 in Disquisitiones Arithmeticae. Leipzig, Germany, 1801. Translated by A. A. Clarke.
New Haven, CT: Yale University Press, 1965.
Kazarinoff, N. D. ``On Who First Proved the Impossibility of Constructing Certain Regular Polygons with Ruler and Compass Alone.''
Amer. Math. Monthly 75, 647-648, 1968.
Ogilvy, C. S. Excursions in Geometry. New York: Dover, pp. 137-138, 1990.
Wantzel, M. L. ``Recherches sur les moyens de reconnaître si un Problème de Géométrie peut se
résoudre avec la règle et le compas.'' J. Math. pures appliq. 1, 366-372, 1836.
|
|
|
© 1996-9 Eric W. Weisstein