|
|
|
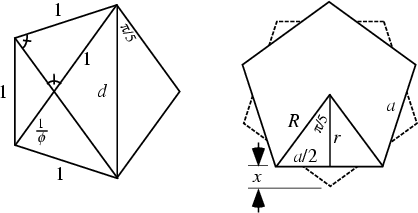
The regular convex 5-gon is called the pentagon. By Similar Triangles in the figure on the
left,
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
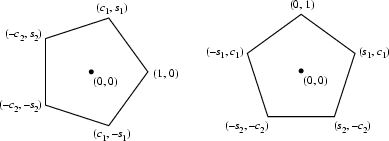
The coordinates of the Vertices relative to the center of the pentagon with unit sides are given as
shown in the above figure, with
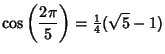 |
(6) | ||
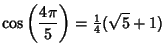 |
(7) | ||
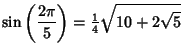 |
(8) | ||
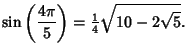 |
(9) |
| (10) | |||
| (11) | |||
| (12) | |||
| (13) |
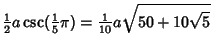 |
(14) | ||
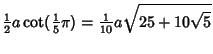 |
(15) | ||
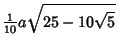 |
(16) | ||
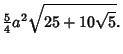 |
(17) |
Five pentagons can be arranged around an identical pentagon to form the first iteration of the ``Pentaflake,''
which itself has the shape of a pentagon with five triangular wedges removed. For a pentagon of side length 1,
the first ring of pentagons has centers at radius ![]() , the second ring at
, the second ring at ![]() , and the
, and the ![]() th at
th at
![]() .
.

In proposition IV.11, Euclid ![]() showed how to inscribe a regular pentagon in a Circle. Ptolemy
showed how to inscribe a regular pentagon in a Circle. Ptolemy ![]() also gave a Ruler and Compass construction for the pentagon in his epoch-making work The Almagest.
While Ptolemy's construction has a Simplicity of 16, a Geometric Construction using Carlyle
Circles can be made with Geometrography symbol
also gave a Ruler and Compass construction for the pentagon in his epoch-making work The Almagest.
While Ptolemy's construction has a Simplicity of 16, a Geometric Construction using Carlyle
Circles can be made with Geometrography symbol
![]() , which has
Simplicity 15 (De Temple 1991).
, which has
Simplicity 15 (De Temple 1991).
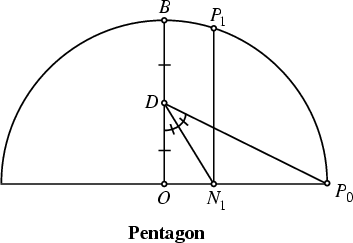
The following elegant construction for the pentagon is due to Richmond (1893). Given a point, a Circle may be
constructed of any desired Radius, and a Diameter drawn through the center. Call the center ![]() , and the right
end of the Diameter
, and the right
end of the Diameter ![]() . The Diameter Perpendicular to the original Diameter may be constructed
by finding the Perpendicular Bisector. Call the upper endpoint of this Perpendicular Diameter
. The Diameter Perpendicular to the original Diameter may be constructed
by finding the Perpendicular Bisector. Call the upper endpoint of this Perpendicular Diameter ![]() . For
the pentagon, find the Midpoint of
. For
the pentagon, find the Midpoint of ![]() and call it
and call it ![]() . Draw
. Draw ![]() , and Bisect
, and Bisect ![]() , calling the intersection point with
, calling the intersection point with ![]()
![]() . Draw
. Draw ![]() Parallel to
Parallel to ![]() , and the first two points of
the pentagon are
, and the first two points of
the pentagon are ![]() and
and ![]() (Coxeter 1969).
(Coxeter 1969).
Madachy (1979) illustrates how to construct a pentagon by folding and knotting a strip of paper.
See also Cyclic Pentagon, Decagon, Dissection, Five Disks Problem, Home Plate, Pentaflake, Pentagram, Polygon, Trigonometry Values Pi/5
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed.
New York: Dover, pp. 95-96, 1987.
Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: Wiley, pp. 26-28, 1969.
De Temple, D. W. ``Carlyle Circles and the Lemoine Simplicity of Polygonal Constructions.'' Amer. Math. Monthly
98, 97-108, 1991.
Dixon, R. Mathographics. New York: Dover, p. 17, 1991.
Dudeney, H. E. Amusements in Mathematics. New York: Dover, p. 38, 1970.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, p. 59, 1979.
Pappas, T. ``The Pentagon, the Pentagram & the Golden Triangle.'' The Joy of Mathematics.
San Carlos, CA: Wide World Publ./Tetra, pp. 188-189, 1989.
Richmond, H. W. ``A Construction for a Regular Polygon of Seventeen Sides.'' Quart. J. Pure Appl. Math. 26, 206-207, 1893.
Wantzel, M. L. ``Recherches sur les moyens de reconnaître si un Problème de Géométrie peut se
résoudre avec la règle et le compas.'' J. Math. pures appliq. 1, 366-372, 1836.
|
|
|
© 1996-9 Eric W. Weisstein