|
|
|
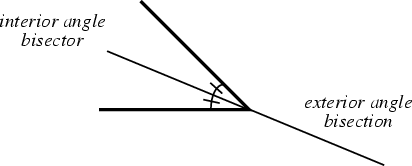
The (interior) bisector of an Angle is the Line or Line Segment which cuts it into two equal Angles on the same ``side'' as the Angle.
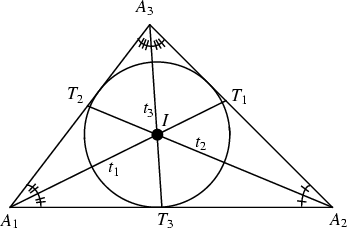
The length of the bisector of Angle ![]() in the above Triangle
in the above Triangle
![]() is given by
is given by
See also Angle Bisector Theorem, Cyclic Quadrangle, Exterior Angle Bisector, Isodynamic Points, Orthocentric System, Steiner-Lehmus Theorem, Trisection
References
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 9-10, 1967.
Dixon, R. Mathographics. New York: Dover, p. 19, 1991.
Mackay, J. S. ``Properties Concerned with the Angular Bisectors of a Triangle.'' Proc. Edinburgh Math. Soc. 13, 37-102, 1895.