|
|
|
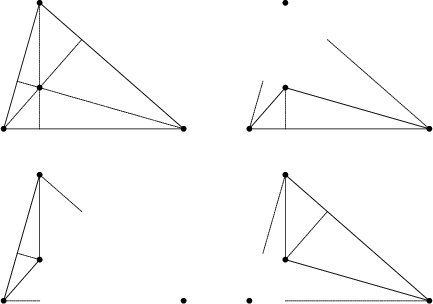
A set of four points, one of which is the Orthocenter of the other three. In an orthocentric system, each point is the Orthocenter of the Triangle of the other three, as illustrated above. The Incenter and Excenters of a Triangle are an orthocentric system. The centers of the Circumcircles of an orthocentric system form another orthocentric system congruent to the first. The sum of the squares of any nonadjacent pair of connectors of an orthocentric system equals the square of the Diameter of the Circumcircle. Orthocentric systems are used to define Orthocentric Coordinates.
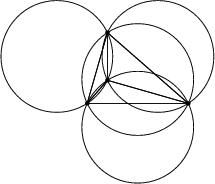
The four Circumcircles of points in an orthocentric system taken three at a time (illustrated above) have equal Radius.
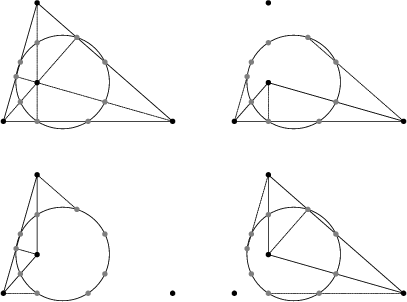
The four triangles of an orthocentric system have a common Nine-Point Circle, illustrated above.
See also Angle Bisector, Circumcircle, Cyclic Quadrangle, Nine-Point Circle, Orthic Triangle, Orthocenter, Orthocentric System, Polar Circle
References
Altshiller-Court, N. College Geometry: A Second Course in Plane Geometry for Colleges and Normal Schools, 2nd ed.
New York: Barnes and Noble, pp. 109-114, 1952.
Johnson, R. A. Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle.
Boston, MA: Houghton Mifflin, pp. 165-176, 1929.