|
|
|
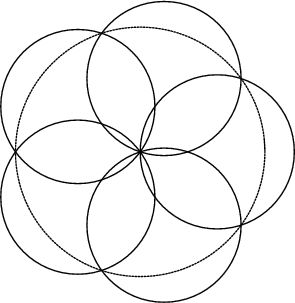
Given five equal Disks placed symmetrically about a given center, what is the smallest
Radius ![]() for which the Radius of the circular Area covered by the five disks is 1? The answer is
for which the Radius of the circular Area covered by the five disks is 1? The answer is
![]() , where
, where ![]() is the Golden Ratio, and the centers
is the Golden Ratio, and the centers ![]() of the disks
of the disks ![]() , ..., 5
are located at
, ..., 5
are located at
![\begin{displaymath}
c_i=\left[{\matrix{{1\over\phi}\cos\left({2\pi i\over 5}\rig...
...\pi i\over 5}\right)\cr}}\right].\hrule width 0pt height 4.2pt
\end{displaymath}](f_1424.gif)
See also Arc, Disk Covering Problem, Flower of Life, Seed of Life
References
Ball, W. W. R. and Coxeter, H. S. M. ``The Five-Disc Problem.''
In Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 97-99, 1987.
Neville, E. H. ``On the Solution of Numerical Functional Equations, Illustrated by an Account of a Popular Puzzle and of its Solution.''
Proc. London Math. Soc. 14, 308-326, 1915.