|
|
|
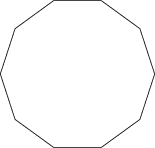
The constructible regular 10-sided Polygon with Schläfli Symbol ![]() . The
Inradius
. The
Inradius ![]() , Circumradius
, Circumradius ![]() , and Area can be computed directly from the formulas for a general
regular Polygon with side length
, and Area can be computed directly from the formulas for a general
regular Polygon with side length ![]() and
and ![]() sides,
sides,
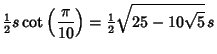 |
(1) | ||
| (2) | |||
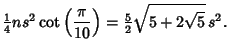 |
(3) |
See also Decagram, Dodecagon, Trigonometry Values Pi/10, Undecagon
References
Dixon, R. Mathographics. New York: Dover, p. 18, 1991.