|
|
|
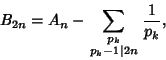
The theorem was rediscovered by Ramanujan ![]() (Hardy 1959, p. 11) and can be proved using p-adic Number.
(Hardy 1959, p. 11) and can be proved using p-adic Number.
See also Bernoulli Number, p-adic Number
References
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, p. 109, 1996.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1959.
Hardy, G. H. and Wright, E. M. ``The Theorem of von Staudt'' and ``Proof of von Staudt's Theorem.'' §7.9-7.10 in
An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 90-93, 1979.
Sloane, N. J. A. Sequence
A000146/M1717
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Staudt, K. G. C. von. ``Beweis eines Lehrsatzes, die Bernoullischen Zahlen betreffend.'' J. reine angew. Math. 21, 372-374, 1840.