Harmonic Divisor Number

A number $n$ for which the Harmonic Mean of the Divisors of $n$, i.e., $nd(n)/\sigma(n)$, is an Integer, where $d(n)$ is the number of Positive integral Divisors of $n$ and $\sigma(n)$ is the Divisor Function. For example, the divisors of $n=140$ are 1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, and 140, giving

$$d(140) = 12$$

$$\sigma(140) = 336$$

$${140d(140)\over\sigma(140)} = {140\cdot 12\over 336}=5,$$

so 140 is a harmonic divisor number. Harmonic divisor numbers are also called Ore Numbers. Garcia (1954) gives the 45 harmonic divisor numbers less than $10^7$. The first few are 1, 6, 140, 270, 672, 1638, ... (Sloane's A007340).

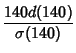For distinct Primes $p$ and $q$, harmonic divisor numbers are equivalent to Even Perfect Numbers for numbers of the form $p^rq$. Mills (1972) proved that if there exists an Odd Positive harmonic divisor number $n$, then $n$ has a prime-Power factor greater than $10^7$.

Another type of number called ``harmonic'' is the Harmonic Number.

See also Divisor Function, Harmonic Number

References

Edgar, H. M. W. ``Harmonic Numbers.'' Amer. Math. Monthly 99, 783-789, 1992.

Garcia, M. ``On Numbers with Integral Harmonic Mean.'' Amer. Math. Monthly 61, 89-96, 1954.

Guy, R. K. ``Almost Perfect, Quasi-Perfect, Pseudoperfect, Harmonic, Weird, Multiperfect and Hyperperfect Numbers.'' §B2 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 45-53, 1994.

Mills, W. H. ``On a Conjecture of Ore.'' Proceedings of the 1972 Number Theory Conference. University of Colorado, Boulder, pp. 142-146, 1972.

Ore, Ø. ``On the Averages of the Divisors of a Number.'' Amer. Math. Monthly 55, 615-619, 1948.

Pomerance, C. ``On a Problem of Ore: Harmonic Numbers.'' Unpublished manuscript, 1973.

Sloane, N. J. A. Sequence A007340/M4299 in ``An On-Line Version of the Encyclopedia of Integer Sequences.'' http://www.research.att.com/~njas/sequences/eisonline.html and extended entry in Sloane, N. J. A. and Plouffe, S. The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.

Zachariou, A. and Zachariou, E. ``Perfect, Semi-Perfect and Ore Numbers.'' Bull. Soc. Math. Gréce (New Ser.) 13, 12-22, 1972.