|
|
|
![]() is defined as the sum of the
is defined as the sum of the ![]() th Powers of the Divisors of
th Powers of the Divisors of ![]() . The
function
. The
function ![]() gives the total number of Divisors of
gives the total number of Divisors of ![]() and is often denoted
and is often denoted ![]() ,
, ![]() ,
,
![]() , or
, or ![]() (Hardy and Wright 1979, pp. 354-355). The first few values of
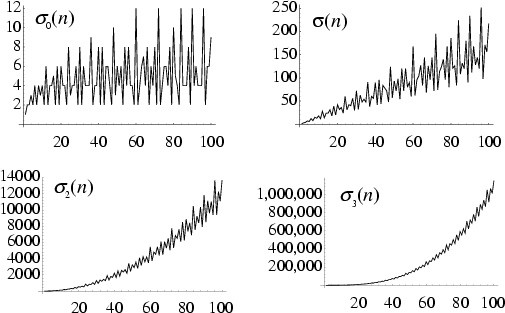
(Hardy and Wright 1979, pp. 354-355). The first few values of ![]() are 1, 2, 2, 3, 2, 4,
2, 4, 3, 4, 2, 6, ... (Sloane's A000005). The function
are 1, 2, 2, 3, 2, 4,
2, 4, 3, 4, 2, 6, ... (Sloane's A000005). The function ![]() is equal to the sum of Divisors of
is equal to the sum of Divisors of
![]() and is often denoted
and is often denoted ![]() . The first few values of
. The first few values of ![]() are 1, 3, 4, 7, 6, 12, 8, 15, 13, 18, ...
(Sloane's A000203). The first few values of
are 1, 3, 4, 7, 6, 12, 8, 15, 13, 18, ...
(Sloane's A000203). The first few values of ![]() are 1, 5, 10, 21, 26, 50, 50, 85, 91, 130, ... (Sloane's A001157). The
first few values of
are 1, 5, 10, 21, 26, 50, 50, 85, 91, 130, ... (Sloane's A001157). The
first few values of ![]() are 1, 9, 28, 73, 126, 252, 344, 585, 757, 1134, ... (Sloane's A001158).
are 1, 9, 28, 73, 126, 252, 344, 585, 757, 1134, ... (Sloane's A001158).
The sum of the Divisors of ![]() excluding
excluding ![]() itself (i.e., the Proper Divisors of
itself (i.e., the Proper Divisors of ![]() ) is called the Restricted Divisor Function and is denoted
) is called the Restricted Divisor Function and is denoted ![]() . The first few values are 0, 1,
1, 3, 1, 6, 1, 7, 4, 8, 1, 16, ... (Sloane's A001065).
. The first few values are 0, 1,
1, 3, 1, 6, 1, 7, 4, 8, 1, 16, ... (Sloane's A001065).
As an illustrative example, consider the number 140, which has Divisors ![]() , 2, 4, 5, 7, 10, 14, 20,
28, 35, 70, and 140 (for a total of
, 2, 4, 5, 7, 10, 14, 20,
28, 35, 70, and 140 (for a total of ![]() of them). Therefore,
of them). Therefore,
| (1) | |||
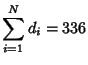 |
(2) | ||
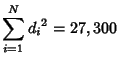 |
(3) | ||
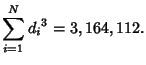 |
(4) |
The ![]() function has the series expansion
function has the series expansion
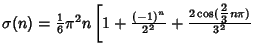
|
|
![$ \left.{+ {2\cos({\textstyle{1\over 2}}n\pi)\over 4^2}+{2[\cos({\textstyle{2\over 5}} n\pi)+\cos({\textstyle{4\over 5}} n\pi)]\over 5^2}+\ldots}\right]\quad$](d2_1286.gif)
|
(5) |
| (6) |
Let a number ![]() have Prime factorization
have Prime factorization
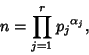 |
(7) |
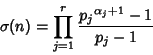 |
(8) |
| (9) |
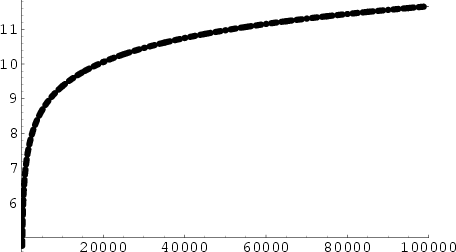
In general,
| (10) |
| (11) |
A curious identity derived using Modular Form theory is given by
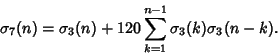 |
(12) |
The asymptotic Summatory Function of
![]() is given by
is given by
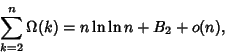 |
(13) |
![\begin{displaymath}
B_2=\gamma+\sum_{p{\rm\ prime}} \left[{\ln(1-p^{-1})+{1\over p-1}}\right]\approx 1.034653
\end{displaymath}](d2_1297.gif) |
(14) |
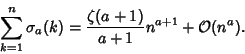 |
(15) |
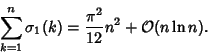 |
(16) |
| (17) |
See also Dirichlet Divisor Problem, Divisor, Factor, Greatest Prime Factor, Gronwall's Theorem, Least Prime Factor, Multiply Perfect Number, Ore's Conjecture, Perfect Number, r(n), Restricted Divisor Function, Silverman Constant, Tau Function, Totient Function, Totient Valence Function, Twin Peaks
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Divisor Functions.'' §24.3.3 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 827, 1972.
Berndt, B. C. Ramanujan's Notebooks: Part I. New York: Springer-Verlag, p. 94, 1985.
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 260-261, 1996.
Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Chelsea,
pp. 279-325, 1952.
Dirichlet, G. L. ``Sur l'usage des séries infinies dans la théorie des nombres.'' J. reine angew. Math. 18, 259-274, 1838.
Erdös, P. ``Ramanujan and I.'' In Proceedings of the International Ramanujan Centenary Conference
held at Anna University, Madras, Dec. 21, 1987. (Ed. K. Alladi). New York: Springer-Verlag, pp. 1-20, 1989.
Guy, R. K. ``Solutions of
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, p. 141,
1959.
Hardy, G. H. and Weight, E. M. An Introduction to the Theory of Numbers, 5th ed.
Oxford, England: Oxford University Press, pp. 354-355, 1979.
Honsberger, R. More Mathematical Morsels. Washington, DC: Math. Assoc. Amer., pp. 250-251, 1991.
Robin, G. ``Grandes valeurs de la fonction somme des diviseurs et hypothese de Riemann.''
J. Math. Pures Appl. 63, 187-213, 1984.
Sloane, N. J. A. Sequences
A000005/M0246,
A000203/M2329
A001065/M2226,
A001157/M3799, and
A001158/M4605,
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Subbarao, M. V. ``On Two Congruences for Primality.'' Pacific J. Math. 52, 261-268, 1974.
![]() ,'' ``Analogs with
,'' ``Analogs with ![]() ,
, ![]() ,''
``Solutions of
,''
``Solutions of
![]() ,'' and ``Solutions of
,'' and ``Solutions of
![]() .'' §B11, B12, B13 and B15 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 67-70, 1994.
.'' §B11, B12, B13 and B15 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 67-70, 1994.
|
|
|
© 1996-9 Eric W. Weisstein