|
|
|
A function ![]() related to the Divisor Function
related to the Divisor Function ![]() , also sometimes called Ramanujan's Tau
Function. It is given by the Generating Function
, also sometimes called Ramanujan's Tau
Function. It is given by the Generating Function
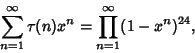 |
(1) |
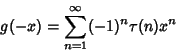 |
(2) |
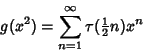 |
(3) |
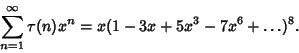 |
(4) |
In Ore's Conjecture, the tau function appears as the number of Divisors of ![]() .
Ramanujan
.
Ramanujan ![]() conjectured and Mordell proved that if
conjectured and Mordell proved that if ![]() , then
, then
| (5) |
| (6) |
| (7) |
Ramanujan ![]() also studied
also studied
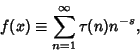 |
(8) |
| (9) |
| (10) |
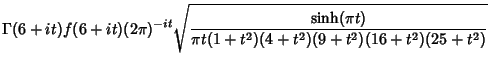 |
(11) | ||
![$\displaystyle -{\textstyle{1\over 2}}i\ln\left[{\Gamma(6+it)\over\Gamma(6-it)}\right]-t\ln(2\pi).$](t_194.gif) |
(12) |
The Summatory tau function is given by
| (13) |
Ramanujan's tau theta function ![]() is a Real function for Real
is a Real function for Real ![]() and is
analogous to the Riemann-Siegel Function
and is
analogous to the Riemann-Siegel Function ![]() . The number of zeros in the critical strip
from
. The number of zeros in the critical strip
from ![]() to
to ![]() is given by
is given by
| (14) |
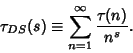 |
(15) |
Ramanujan's ![]() function is defined by
function is defined by
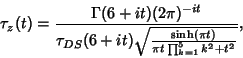 |
(16) |
See also Ore's Conjecture, Tau Conjecture, Tau-Dirichlet Series
References
Hardy, G. H. ``Ramanujan's Function
Sloane, N. J. A. Sequence
A000594/M5153
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
![]() .'' Ch. 10 in
Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1959.
.'' Ch. 10 in
Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1959.
|
|
|
© 1996-9 Eric W. Weisstein