Define the Harmonic Mean of the Divisors of 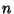
where 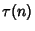 is the Tau Function (the number of Divisors of
is the Tau Function (the number of Divisors of 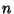 ). If
). If 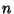 is a Perfect
Number,
is a Perfect
Number, 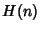 is an Integer. Ore conjectured that if
is an Integer. Ore conjectured that if 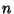 is Odd, then
is Odd, then 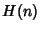 is not an Integer. This
implies that no Odd Perfect Numbers exist.
is not an Integer. This
implies that no Odd Perfect Numbers exist.
See also Harmonic Divisor Number, Harmonic Mean, Perfect Number, Tau Function
© 1996-9 Eric W. Weisstein
1999-05-26
![]()