|
|
|
The harmonic mean
![]() of
of ![]() points
points ![]() (where
(where ![]() , ...,
, ..., ![]() ) is
) is
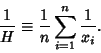 |
(1) |
| (2) |
| (3) |
Hoehn and Niven (1985) show that
| (4) |
See also Arithmetic Mean, Arithmetic-Geometric Mean, Geometric Mean, Harmonic-Geometric Mean, Root-Mean-Square
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 10, 1972.
Hoehn, L. and Niven, I. ``Averages on the Move.'' Math. Mag. 58, 151-156, 1985.