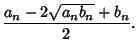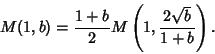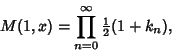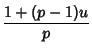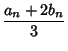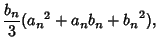The arithmetic-geometric mean (AGM) 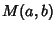 of two numbers
of two numbers 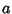 and
and 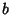 is defined by starting with
is defined by starting with 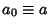 and
and
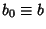 , then iterating
, then iterating
until 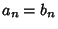 .
. 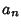 and
and 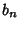 converge towards each other since
converge towards each other since
But
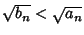 , so
, so
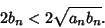 |
(4) |
Now, add
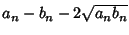 to each side
to each side
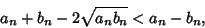 |
(5) |
so
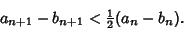 |
(6) |
The AGM is very useful in computing the values of complete Elliptic Integrals and can also be
used for finding the Inverse Tangent. The special value
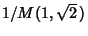 is called Gauss's Constant.
is called Gauss's Constant.
The AGM has the properties
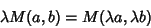 |
(7) |
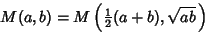 |
(8) |
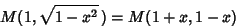 |
(9) |
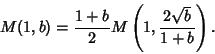 |
(10) |
The Legendre form is given by
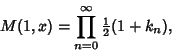 |
(11) |
where 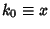 and
and
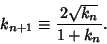 |
(12) |
Solutions to the differential equation
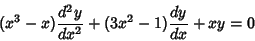 |
(13) |
are given by
![$[M(1+x,1-x)]^{-1}$](a_1627.gif) and
and ![$[M(1,x)]^{-1}$](a_1628.gif) .
.
A generalization of the Arithmetic-Geometric Mean is
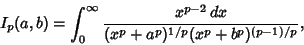 |
(14) |
which is related to solutions of the differential equation
![\begin{displaymath}
x(1-x^p)Y''+[1-(p+1)x^p]Y'-(p-1)x^{p-1}Y=0.
\end{displaymath}](a_1630.gif) |
(15) |
When 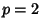 or
or 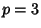 , there is a modular transformation for the solutions of (15) that are bounded as
, there is a modular transformation for the solutions of (15) that are bounded as 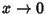 .
Letting
.
Letting 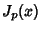 be one of these solutions, the transformation takes the form
be one of these solutions, the transformation takes the form
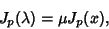 |
(16) |
where
and
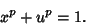 |
(19) |
The case 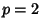 gives the Arithmetic-Geometric Mean, and
gives the Arithmetic-Geometric Mean, and 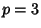 gives a cubic relative discussed by Borwein and
Borwein (1990, 1991) and Borwein (1996) in which, for
gives a cubic relative discussed by Borwein and
Borwein (1990, 1991) and Borwein (1996) in which, for 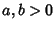 and
and 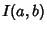 defined by
defined by
![\begin{displaymath}
I(a,b)=\int_0^\infty {t\,dt\over [(a^3+t^3)(b^3+t^3)^2]^{1/3}},
\end{displaymath}](a_1642.gif) |
(20) |
![\begin{displaymath}
I(a,b)=I\left({{a+2b\over 3}, \left[{{b\over 3} (a^2+ab+b^2)}\right]}\right).
\end{displaymath}](a_1643.gif) |
(21) |
For iteration with 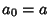 and
and 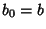 and
and
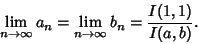 |
(24) |
Modular transformations are known when 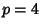 and
and 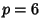 , but they do not give identities for
, but they do not give identities for 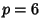 (Borwein 1996).
(Borwein 1996).
See also Arithmetic-Harmonic Mean
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``The Process of the Arithmetic-Geometric Mean.'' §17.6 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 571 ad 598-599, 1972.
Borwein, J. M. Problem 10281. ``A Cubic Relative of the AGM.'' Amer. Math. Monthly 103, 181-183, 1996.
Borwein, J. M. and Borwein, P. B. ``A Remarkable Cubic Iteration.''
In Computational Method & Function Theory: Proc. Conference Held in Valparaiso, Chile, March 13-18, 1989
(Ed. A. Dold, B. Eckmann, F. Takens, E. B Saff, S. Ruscheweyh, L. C. Salinas, L. C., and R. S. Varga). New York: Springer-Verlag, 1990.
Borwein, J. M. and Borwein, P. B. ``A Cubic Counterpart of Jacobi's Identity and the AGM.''
Trans. Amer. Math. Soc. 323, 691-701, 1991.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T.
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge
University Press, pp. 906-907, 1992.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() of two numbers
of two numbers ![]() and
and ![]() is defined by starting with
is defined by starting with ![]() and
and
![]() , then iterating
, then iterating