An elliptic integral is an Integral of the form
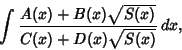 |
(1) |
or
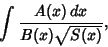 |
(2) |
where 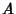 ,
, 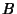 ,
, 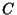 , and
, and 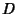 are Polynomials in
are Polynomials in 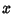 and
and 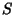 is a Polynomial of degree 3 or 4. Another form is
is a Polynomial of degree 3 or 4. Another form is
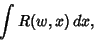 |
(3) |
where 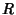 is a Rational Function of
is a Rational Function of 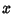 and
and 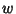 ,
, 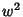 is a function of
is a function of 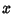 Cubic or
Quadratic in
Cubic or
Quadratic in 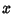 ,
, 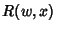 contains at least one Odd Power of
contains at least one Odd Power of 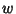 , and
, and 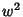 has no
repeated factors.
has no
repeated factors.
Elliptic integrals can be viewed as generalizations of the inverse Trigonometric Functions and provide
solutions to a wider class of problems. For instance, while the Arc Length of a Circle is given as a simple
function of the parameter, computing the Arc Length of an Ellipse requires an elliptic integral. Similarly,
the position of a pendulum  is given by a Trigonometric Function as a
function of time for small angle oscillations, but the full solution for arbitrarily large displacements requires the use
of elliptic integrals. Many other problems in electromagnetism and gravitation are solved by elliptic integrals.
is given by a Trigonometric Function as a
function of time for small angle oscillations, but the full solution for arbitrarily large displacements requires the use
of elliptic integrals. Many other problems in electromagnetism and gravitation are solved by elliptic integrals.
A very useful class of functions known as Elliptic Functions is obtained by inverting
elliptic integrals to obtain generalizations of the trigonometric functions. Elliptic Functions
(among which the Jacobi Elliptic Functions and Weierstraß Elliptic Function are the two most common forms) provide a powerful tool for analyzing many deep problems in Number Theory,
as well as other areas of mathematics.
All elliptic integrals can be written in terms of three ``standard'' types. To see this, write
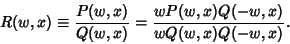 |
(4) |
But since 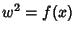 ,
,
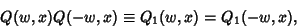 |
(5) |
then
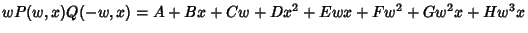
|
|
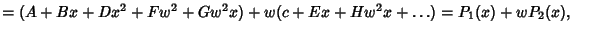
|
(6) |
so
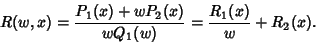 |
(7) |
But any function
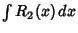 can be evaluated in terms of elementary functions, so the only portion that need be
considered is
can be evaluated in terms of elementary functions, so the only portion that need be
considered is
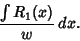 |
(8) |
Now, any quartic can be expressed as 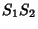 where
where
The Coefficients here are real, since pairs of Complex Roots are
Complex Conjugates
If all four Roots are real, they must be arranged so as not to interleave (Whittaker and Watson 1990, p. 514). Now define a
quantity 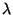 such that
such that
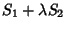
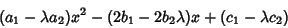 |
(12) |
is a Square Number and
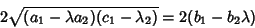 |
(13) |
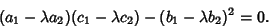 |
(14) |
Call the Roots of this equation 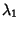 and
and 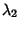 , then
, then
Taking (15)-(16) and
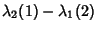 gives
gives
Solving gives
so we have
![\begin{displaymath}
w^2=S_1S_2 = [A_1(x-\alpha)^2+B_1(x-\beta)^2][A^2(x-\alpha)^2+B^2(x-\beta)^2].
\end{displaymath}](e_899.gif) |
(21) |
Now let
so
and
Now let
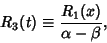 |
(27) |
so
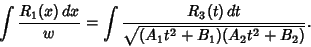 |
(28) |
Rewriting the Even and Odd parts
gives
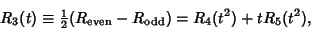 |
(31) |
so we have
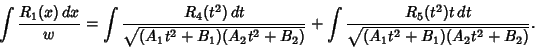 |
(32) |
Letting
reduces the second integral to
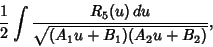 |
(35) |
which can be evaluated using elementary functions. The first integral can then be reduced by Integration by Parts to
one of the three Legendre elliptic integrals (also called Legendre-Jacobi Elliptic Integrals),
known as incomplete elliptic integrals of the first, second, and third kind, denoted 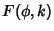 ,
, 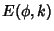 , and
, and
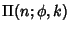 , respectively (von Kármán and Biot 1940, Whittaker and Watson 1990, p. 515). If
, respectively (von Kármán and Biot 1940, Whittaker and Watson 1990, p. 515). If 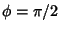 , then the integrals
are called complete elliptic integrals and are denoted
, then the integrals
are called complete elliptic integrals and are denoted 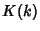 ,
, 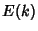 ,
, 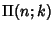 .
.
Incomplete elliptic integrals are denoted using a Modulus 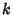 , Parameter
, Parameter
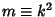 , or Modular Angle
, or Modular Angle
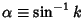 . An elliptic integral is written
. An elliptic integral is written 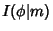 when the
Parameter is used,
when the
Parameter is used, 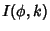 when the Modulus is used, and
when the Modulus is used, and
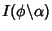 when the Modular Angle is used. Complete elliptic integrals are defined when
when the Modular Angle is used. Complete elliptic integrals are defined when 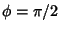 and
can be expressed using the expansion
and
can be expressed using the expansion
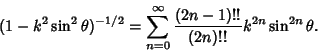 |
(36) |
An elliptic integral in standard form
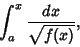 |
(37) |
where
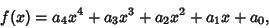 |
(38) |
can be computed analytically (Whittaker and Watson 1990, p. 453) in terms
of the Weierstraß Elliptic Function with
invariants
If 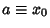 is a root of
is a root of 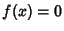 , then the solution is
, then the solution is
![\begin{displaymath}
x=x_0+{\textstyle{1\over 4}}f'(x_0)[\wp(z;g_2,g_3)-{\textstyle{1\over 24}}f''(x_0)]^{-1}.
\end{displaymath}](e_948.gif) |
(41) |
For an arbitrary lower bound,
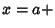
|
|
![${\sqrt{f(a)}\wp'(z)+{\textstyle{1\over 2}}f'(a)[\wp(z)-{\textstyle{1\over 24}}f...
...\wp(z)-{\textstyle{1\over 24}}f''(a)]^2-{\textstyle{1\over 48}}f(a)f^{(a)}(a)},$](e_950.gif)
|
|
|
|
(42) |
where
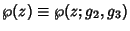 is a
Weierstraß Elliptic Function.
is a
Weierstraß Elliptic Function.
A generalized elliptic integral can be defined by the function
(Borwein and Borwein 1987). Now let
But
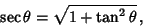 |
(47) |
so
and
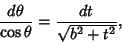 |
(49) |
and the equation becomes
Now we make the further substitution
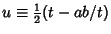 . The differential becomes
. The differential becomes
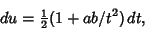 |
(51) |
but 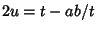 , so
, so
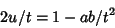 |
(52) |
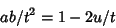 |
(53) |
and
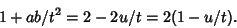 |
(54) |
However, the left side is always positive, so
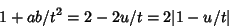 |
(55) |
and the differential is
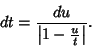 |
(56) |
We need to take some care with the limits of integration. Write (50) as
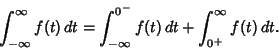 |
(57) |
Now change the limits to those appropriate for the 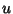 integration
integration
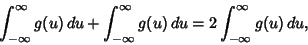 |
(58) |
so we have picked up a factor of 2 which must be included. Using this fact and plugging (56) in (50) therefore
gives
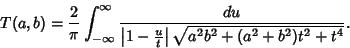 |
(59) |
Now note that
Plug (62) into (59) to obtain
But
so
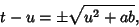 |
(67) |
and (63) becomes
We have therefore demonstrated that
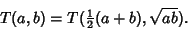 |
(69) |
We can thus iterate
as many times as we wish, without changing the value of the integral. But this iteration is the same as and therefore
converges to the Arithmetic-Geometric Mean, so the iteration terminates at
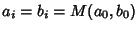 , and we have
, and we have
Complete elliptic integrals arise in finding the arc length of an Ellipse and the period of a
pendulum.  They also arise in a natural way from the theory of Theta Functions. Complete elliptic integrals can be computed using a procedure involving the Arithmetic-Geometric Mean. Note
that
They also arise in a natural way from the theory of Theta Functions. Complete elliptic integrals can be computed using a procedure involving the Arithmetic-Geometric Mean. Note
that
So we have
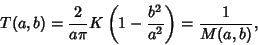 |
(74) |
where 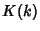 is the complete Elliptic Integral of the First Kind. We are free to let
is the complete Elliptic Integral of the First Kind. We are free to let
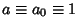 and
and
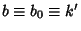 , so
, so
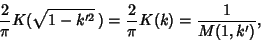 |
(75) |
since
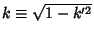 , so
, so
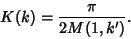 |
(76) |
But the Arithmetic-Geometric Mean is defined by
where
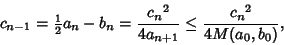 |
(80) |
so we have
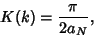 |
(81) |
where 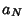 is the value to which
is the value to which 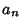 converges. Similarly, taking instead
converges. Similarly, taking instead 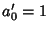 and
and 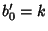 gives
gives
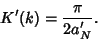 |
(82) |
Borwein and Borwein (1987) also show that defining
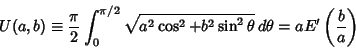 |
(83) |
leads to
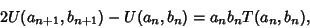 |
(84) |
so
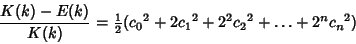 |
(85) |
for 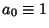 and
and 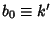 , and
, and
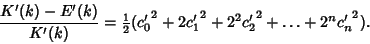 |
(86) |
The elliptic integrals satisfy a large number of identities. The complementary functions and moduli are defined by
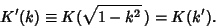 |
(87) |
Use the identity of generalized elliptic integrals
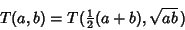 |
(88) |
to write
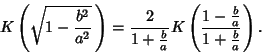 |
(90) |
Define
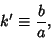 |
(91) |
and use
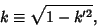 |
(92) |
so
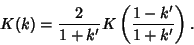 |
(93) |
Now letting
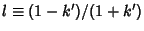 gives
gives
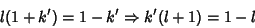 |
(94) |
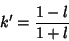 |
(95) |
and
Writing 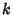 instead of
instead of 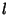 ,
,
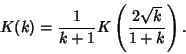 |
(98) |
Similarly, from Borwein and Borwein (1987),
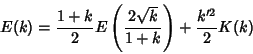 |
(99) |
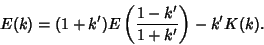 |
(100) |
Expressions in terms of the complementary function can be derived from interchanging the moduli and their complements in
(93), (98), (99), and (100).
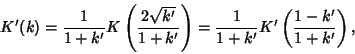 |
(102) |
and
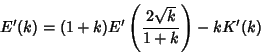 |
(103) |
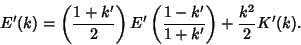 |
(104) |
Taking the ratios
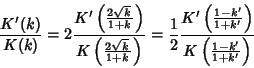 |
(105) |
gives the Modular Equation of degree 2. It is also true that
![\begin{displaymath}
K(x)={4\over (1+\sqrt{x'})^2} K\left({\left[{1-{\root 4\of {1-x^4}}\over 1+{\root 4\of {1-x^4}}\,}\right]^2}\right).
\end{displaymath}](e_1058.gif) |
(106) |
See also Abelian Integral, Amplitude, Argument (Elliptic Integral), Characteristic (Elliptic
Integral), Delta Amplitude, Elliptic Function, Elliptic Integral of the First Kind, Elliptic
Integral of the Second Kind, Elliptic Integral of the Third Kind, Elliptic Integral Singular Value, Heuman
Lambda Function, Jacobi Zeta Function, Modular Angle, Modulus (Elliptic Integral), Nome,
Parameter
References
 Elliptic Integrals
Elliptic Integrals
Abramowitz, M. and Stegun, C. A. (Eds.). ``Elliptic Integrals.'' Ch. 17 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 587-607, 1972.
Arfken, G. ``Elliptic Integrals.'' §5.8 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL:
Academic Press, pp. 321-327, 1985.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity.
New York: Wiley, 1987.
Hancock, H. Elliptic Integrals. New York: Wiley, 1917.
King, L. V. The Direct Numerical Calculation of Elliptic Functions and Integrals. London: Cambridge University Press, 1924.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T.
``Elliptic Integrals and Jacobi Elliptic Functions.'' §6.11 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 254-263, 1992.
Prudnikov, A. P.; Brychkov, Yu. A.; and Marichev, O. I. Integrals and Series, Vol. 1: Elementary Functions.
New York: Gordon & Breach, 1986.
Timofeev, A. F. Integration of Functions. Moscow and Leningrad: GTTI, 1948.
von Kármán, T. and Biot, M. A.
Mathematical Methods in Engineering: An Introduction to the Mathematical Treatment of Engineering Problems.
New York: McGraw-Hill, p. 121, 1940.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England:
Cambridge University Press, 1990.
© 1996-9 Eric W. Weisstein
1999-05-25
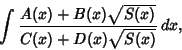
![]() is given by a Trigonometric Function as a
function of time for small angle oscillations, but the full solution for arbitrarily large displacements requires the use
of elliptic integrals. Many other problems in electromagnetism and gravitation are solved by elliptic integrals.
is given by a Trigonometric Function as a
function of time for small angle oscillations, but the full solution for arbitrarily large displacements requires the use
of elliptic integrals. Many other problems in electromagnetism and gravitation are solved by elliptic integrals.
![$\displaystyle \left[{\sqrt{(a_1-\lambda_1a_2)x}+\sqrt{c_1-\lambda c_2}\,}\right]^2$](e_883.gif)
![$\displaystyle \left[{\sqrt{(a_1-\lambda_1a_2)x}+\sqrt{c_1-\lambda c_2}\,}\right]^2$](e_883.gif)
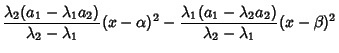
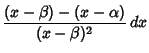
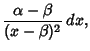
![$\displaystyle (x-\beta)^4\left[{A_1\left({x-\alpha\over x-\beta}\right)^2+B_1}\right]\left[{A_2\left({x-\alpha\over x-\beta}\right)+B_2}\right]$](e_907.gif)
![$\displaystyle \left[{{(x-\beta)^2\over \alpha-\beta} dt}\right]{1\over (x-\beta)^2\sqrt{(A_1t^2+B_1)(A_2t^2+B_2)}}$](e_912.gif)
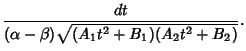
![]() , Parameter
, Parameter
![]() , or Modular Angle
, or Modular Angle
![]() . An elliptic integral is written
. An elliptic integral is written ![]() when the
Parameter is used,
when the
Parameter is used, ![]() when the Modulus is used, and
when the Modulus is used, and
![]() when the Modular Angle is used. Complete elliptic integrals are defined when
when the Modular Angle is used. Complete elliptic integrals are defined when ![]() and
can be expressed using the expansion
and
can be expressed using the expansion
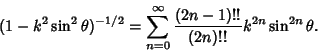
![${\sqrt{f(a)}\wp'(z)+{\textstyle{1\over 2}}f'(a)[\wp(z)-{\textstyle{1\over 24}}f...
...\wp(z)-{\textstyle{1\over 24}}f''(a)]^2-{\textstyle{1\over 48}}f(a)f^{(a)}(a)},$](e_950.gif)
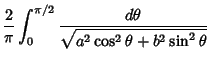
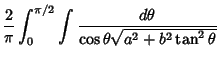
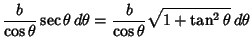
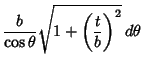
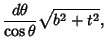
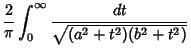
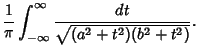
}}$](e_988.gif)
}}.$](e_989.gif)
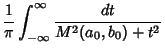
![$\displaystyle {1\over \pi M(a_0,b_0)} \left[{\tan^{-1}\left({t\over M(a_0,b_0)}\right)}\right]^\infty_{-\infty}$](e_999.gif)
![]() They also arise in a natural way from the theory of Theta Functions. Complete elliptic integrals can be computed using a procedure involving the Arithmetic-Geometric Mean. Note
that
They also arise in a natural way from the theory of Theta Functions. Complete elliptic integrals can be computed using a procedure involving the Arithmetic-Geometric Mean. Note
that
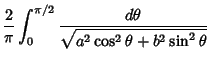
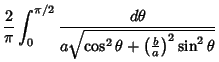
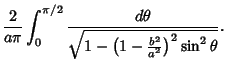
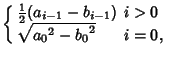
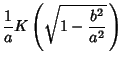
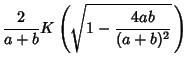
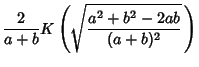
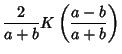
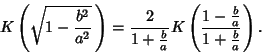
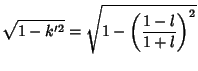
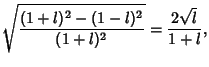
![$\displaystyle {1\over 2}\left({1+{1-l\over 1+l}}\right)= {1\over 2}\left[{(1+l)+(1-l)\over 1+l}\right]$](e_1044.gif)
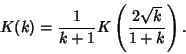
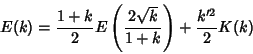
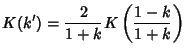
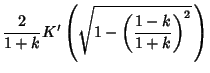
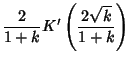
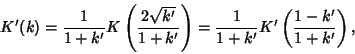
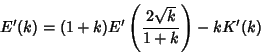
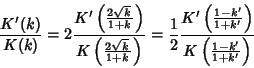
![\begin{displaymath}
K(x)={4\over (1+\sqrt{x'})^2} K\left({\left[{1-{\root 4\of {1-x^4}}\over 1+{\root 4\of {1-x^4}}\,}\right]^2}\right).
\end{displaymath}](e_1058.gif)
![]() Elliptic Integrals
Elliptic Integrals