Let the Modulus 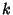 satisfy
satisfy 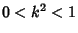 . (This may also be written in terms of the
Parameter
. (This may also be written in terms of the
Parameter 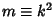 or Modular Angle
or Modular Angle
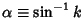 .) The incomplete elliptic integral of the
first kind is then defined as
.) The incomplete elliptic integral of the
first kind is then defined as
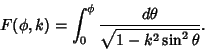 |
(1) |
Let
Let
so the integral can also be written as
where
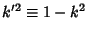 is the complementary Modulus.
is the complementary Modulus.
The integral
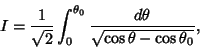 |
(9) |
which arises in computing the period of a pendulum,  is also an elliptic integral of the first
kind. Use
is also an elliptic integral of the first
kind. Use
to write
so
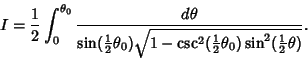 |
(13) |
Now let
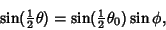 |
(14) |
so the angle 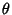 is transformed to
is transformed to
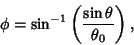 |
(15) |
which ranges from 0 to 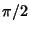 as
as 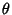 varies from 0 to
varies from 0 to 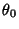 . Taking the differential gives
. Taking the differential gives
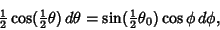 |
(16) |
or
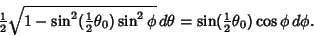 |
(17) |
Plugging this in gives
so
 |
(19) |
Making the slightly different substitution  , so
, so
 leads to an equivalent, but more complicated
expression involving an incomplete elliptic function of the first kind,
leads to an equivalent, but more complicated
expression involving an incomplete elliptic function of the first kind,
Therefore, we have proven the identity
 |
(21) |
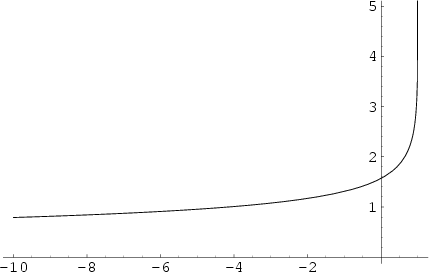
The complete elliptic integral of the first kind, illustrated above as a function of 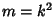 , is defined by
, is defined by
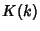 |
 |
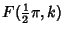 |
(22) |
| |
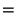 |
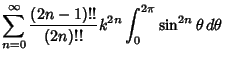 |
(23) |
| |
 |
 |
(24) |
| |
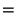 |
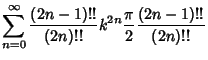 |
|
| |
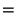 |
![$\displaystyle {\pi\over 2}\sum_{n=0}^\infty \left[{(2n-1)!!\over (2n)!!}\right]^2 k^{2n}$](e_1106.gif) |
(25) |
| |
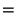 |
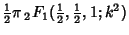 |
(26) |
| |
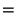 |
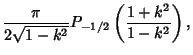 |
(27) |
where
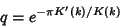 |
(28) |
is the Nome (for 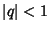 ),
),
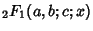 is the Hypergeometric Function, and
is the Hypergeometric Function, and 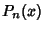 is a Legendre
Polynomial.
is a Legendre
Polynomial. 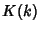 satisfies the Legendre Relation
satisfies the Legendre Relation
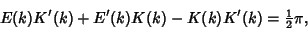 |
(29) |
where 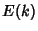 and
and 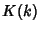 are complete elliptic integrals of the first and Second Kinds, and
are complete elliptic integrals of the first and Second Kinds, and 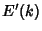 and
and 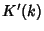 are the complementary integrals. The modulus
are the complementary integrals. The modulus 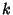 is often suppressed for conciseness, so that
is often suppressed for conciseness, so that
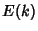 and
and 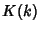 are often simply written
are often simply written 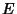 and
and 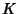 , respectively.
, respectively.
The Derivative of 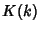 is
is
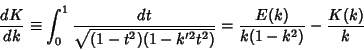 |
(30) |
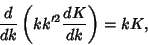 |
(31) |
so
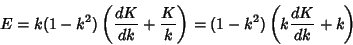 |
(32) |
(Whittaker and Watson 1990, pp. 499 and 521).
See also Amplitude, Characteristic (Elliptic Integral), Elliptic Integral Singular Value, Gauss's
Transformation, Landen's Transformation, Legendre Relation, Modular Angle, Modulus (Elliptic
Integral), Parameter
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Elliptic Integrals.'' Ch. 17 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 587-607, 1972.
Spanier, J. and Oldham, K. B. ``The Complete Elliptic Integrals 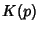 and
and 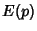 '' and
``The Incomplete Elliptic Integrals
'' and
``The Incomplete Elliptic Integrals 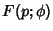 and
and 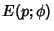 .''
Chs. 61-62 in An Atlas of Functions.
Washington, DC: Hemisphere, pp. 609-633, 1987.
.''
Chs. 61-62 in An Atlas of Functions.
Washington, DC: Hemisphere, pp. 609-633, 1987.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England:
Cambridge University Press, 1990.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() satisfy
satisfy ![]() . (This may also be written in terms of the
Parameter
. (This may also be written in terms of the
Parameter ![]() or Modular Angle
or Modular Angle
![]() .) The incomplete elliptic integral of the
first kind is then defined as
.) The incomplete elliptic integral of the
first kind is then defined as
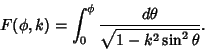
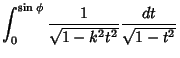
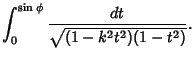
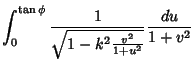
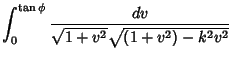
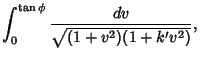
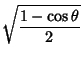
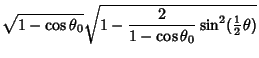
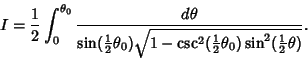
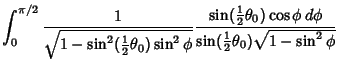
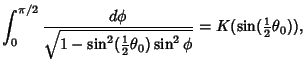
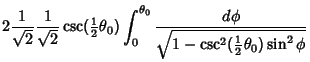
![]() , is defined by
, is defined by
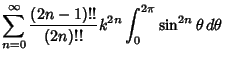
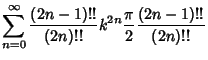
![$\displaystyle {\pi\over 2}\sum_{n=0}^\infty \left[{(2n-1)!!\over (2n)!!}\right]^2 k^{2n}$](e_1106.gif)
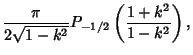
![]() is
is
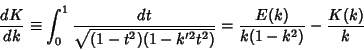
![]() and
and ![]() '' and
``The Incomplete Elliptic Integrals
'' and
``The Incomplete Elliptic Integrals ![]() and
and ![]() .''
Chs. 61-62 in An Atlas of Functions.
Washington, DC: Hemisphere, pp. 609-633, 1987.
.''
Chs. 61-62 in An Atlas of Functions.
Washington, DC: Hemisphere, pp. 609-633, 1987.