|
|
|
When the Modulus ![]() has a singular value, the complete elliptic integrals may be
computed in analytic form in terms of Gamma Functions. Abel
has a singular value, the complete elliptic integrals may be
computed in analytic form in terms of Gamma Functions. Abel ![]() (quoted in Whittaker and
Watson 1990, p. 525) proved that whenever
(quoted in Whittaker and
Watson 1990, p. 525) proved that whenever
| (1) |
A Modulus ![]() such that
such that
| (2) |
The following table gives the values of ![]() for small integral
for small integral ![]() in terms of
Gamma Functions.
in terms of
Gamma Functions.

where ![]() is the Gamma Function and
is the Gamma Function and ![]() is an algebraic number (Borwein and Borwein 1987, p. 298).
is an algebraic number (Borwein and Borwein 1987, p. 298).
Borwein and Zucker (1992) give amazing expressions for singular values of complete elliptic integrals in terms
of Central Beta Functions
| (3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
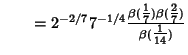
|
|
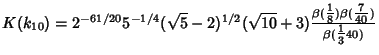
|
|
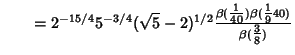
|
|
|
|
|
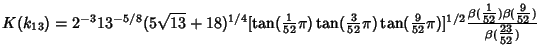
|
|
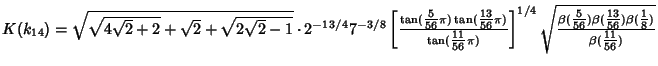
|
|
|
|
|
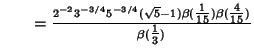
|
|
![$K(k_{17})=C_2\left[{\beta({\textstyle{1\over 68}})\beta({\textstyle{3\over 68}}...
...ver\beta({\textstyle{5\over 68}})\beta({\textstyle{15\over 68}})}\right]^{1/4},$](e_1184.gif)
|
| (4) |
Using the Elliptic Alpha Function, the Elliptic Integrals of the Second Kind can also be found from
![$\displaystyle {\pi\over 4\sqrt{r}K}+\left[{1-{\alpha(r)\over\sqrt{r}}}\right]K$](e_1189.gif) |
(5) | ||
| (6) |
| (7) |
See also Central Beta Function, Elliptic Alpha Function, Elliptic Delta Function, Elliptic Integral of the First Kind, Elliptic Integral of the Second Kind, Elliptic Lambda Function, Gamma Function, Modulus (Elliptic Integral)
References
Abel, N. H. ``Recherches sur les fonctions elliptiques.'' J. reine angew. Math. 3, 160-190, 1828.
Reprinted in Abel, N. H. Oeuvres Completes (Ed. L. Sylow and S. Lie). New York: Johnson Reprint Corp., p. 377, 1988.
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity.
New York: Wiley, pp. 139 and 298, 1987.
Borwein, J. M. and Zucker, I. J. ``Elliptic Integral Evaluation of the Gamma Function at Rational Values of Small
Denominator.'' IMA J. Numerical Analysis 12, 519-526, 1992.
Bowman, F. Introduction to Elliptic Functions, with Applications. New York: Dover, pp. 75, 95, and 98, 1961.
Glasser, M. L. and Wood, V. E. ``A Closed Form Evaluation of the Elliptic Integral.'' Math. Comput. 22, 535-536, 1971.
Selberg, A. and Chowla, S. ``On Epstein's Zeta-Function.'' J. Reine. Angew. Math. 227, 86-110, 1967.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge
University Press, pp. 524-528, 1990.
Wrigge, S. ``An Elliptic Integral Identity.'' Math. Comput. 27, 837-840, 1973.
Zucker, I. J. ``The Evaluation in Terms of
![]() Weisstein, E. W. ``Elliptic Singular Values.'' Mathematica notebook EllipticSingular.m.
Weisstein, E. W. ``Elliptic Singular Values.'' Mathematica notebook EllipticSingular.m.
![]() -Functions of the Periods of Elliptic Curves Admitting Complex
Multiplication.'' Math. Proc. Cambridge Phil. Soc. 82, 111-118, 1977.
-Functions of the Periods of Elliptic Curves Admitting Complex
Multiplication.'' Math. Proc. Cambridge Phil. Soc. 82, 111-118, 1977.
|
|
|
© 1996-9 Eric W. Weisstein