|
|
|
Let the Modulus ![]() satisfy
satisfy ![]() . (This may also be written in terms of
the Parameter
. (This may also be written in terms of
the Parameter ![]() or Modular Angle
or Modular Angle
![]() .) The incomplete elliptic integral
of the second kind is then defined as
.) The incomplete elliptic integral
of the second kind is then defined as
| (1) |
| (2) |
| (3) | |||
| (4) |
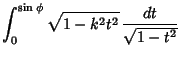 |
|||
 |
(5) |
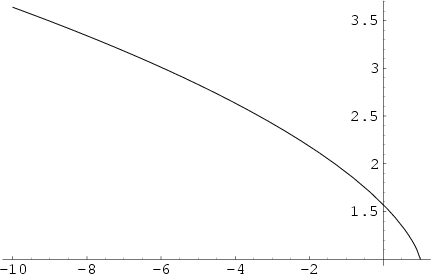
The complete elliptic integral of the second kind, illustrated above as a function of the Parameter ![]() ,
is defined by
,
is defined by
| (6) | |||
![$\displaystyle {\pi\over 2}\left\{{1 - \sum_{n=1}^\infty \left[{(2n-1)!!\over (2n)!!)}\right]^2 {k^{2n}\over 2n-1}}\right\}$](e_1135.gif) |
(7) | ||
| (8) | |||
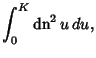 |
(9) |
| (10) |
| (11) |
| (12) |
| (13) |
See also Elliptic Integral of the First Kind, Elliptic Integral of the Third Kind, Elliptic Integral Singular Value
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Elliptic Integrals.'' Ch. 17 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 587-607, 1972.
Spanier, J. and Oldham, K. B. ``The Complete Elliptic Integrals
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England:
Cambridge University Press, 1990.
![]() and
and ![]() '' and
``The Incomplete Elliptic Integrals
'' and
``The Incomplete Elliptic Integrals ![]() and
and ![]() .''
Chs. 61 and 62 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 609-633, 1987.
.''
Chs. 61 and 62 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 609-633, 1987.
|
|
|
© 1996-9 Eric W. Weisstein