|
|
|
Let ![]() . The incomplete elliptic integral of the third kind is then defined as
. The incomplete elliptic integral of the third kind is then defined as
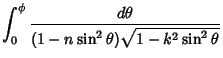 |
(1) | ||
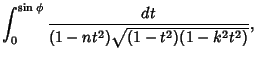 |
(2) |
The complete elliptic integral of the second kind
| (3) |
See also Elliptic Integral of the First Kind, Elliptic Integral of the Second Kind, Elliptic Integral Singular Value
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Elliptic Integrals'' and ``Elliptic Integrals of the Third Kind.''
Ch. 17 and §17.7 in Handbook of Mathematical Functions with Formulas,
Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 587-607, 1972.