|
|
|
An extension of the Jacobi Symbol ![]() to all Integers. It can be computed using the
normal rules for the Jacobi Symbol
to all Integers. It can be computed using the
normal rules for the Jacobi Symbol
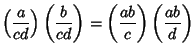 |
|||
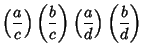 |
(1) |
| (2) |
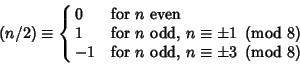 |
(3) |
 |
(4) |
The Kronecker Symbol is a Real Character modulo ![]() , and
is, in fact, essentially the only type of Real primitive character (Ayoub 1963).
, and
is, in fact, essentially the only type of Real primitive character (Ayoub 1963).
See also Character (Number Theory), Class Number, Dirichlet L-Series, Jacobi Symbol, Legendre Symbol
References
Ayoub, R. G. An Introduction to the Analytic Theory of Numbers. Providence, RI: Amer. Math. Soc., 1963.
Cohn, H. Advanced Number Theory. New York: Dover, p. 35, 1980.