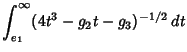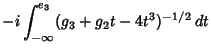The Weierstraß elliptic functions are elliptic functions which, unlike the Jacobi Elliptic Functions, have a
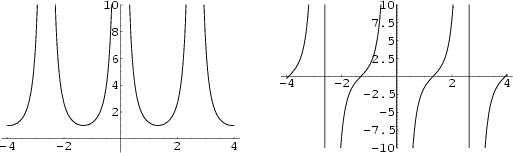
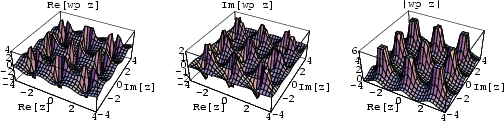
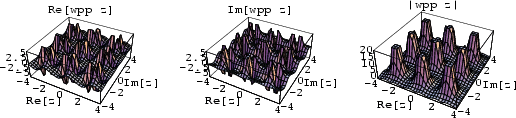
second-order Pole at 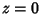 . The above plots show the Weierstraß elliptic function
. The above plots show the Weierstraß elliptic function 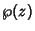 and its derivative
and its derivative
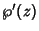 for invariants (defined below) of
for invariants (defined below) of 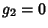 and
and 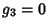 . Weierstraß elliptic functions are denoted
. Weierstraß elliptic functions are denoted 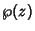 and
can be defined by
and
can be defined by
![\begin{displaymath}
\wp(z) = {1\over z^2} + \setbox0=\hbox{$\scriptstyle{m, n=-\...
...a_1-2n\omega_2)^2}-{1\over (2m\omega_1+2n\omega_2)^2}}\right].
\end{displaymath}](w_475.gif) |
(1) |
Write
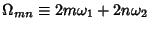 . Then this can be written
. Then this can be written
![\begin{displaymath}
\wp(z)=z^{-2}+\setbox0=\hbox{$\scriptstyle{m, n}$}\setbox2=\...
...}'}_{\kern-\wd4 m, n} [(z-\Omega_{mn})^{-2}-\Omega_{mn}^{-2}].
\end{displaymath}](w_477.gif) |
(2) |
An equivalent definition which converges more rapidly is
![\begin{displaymath}
\wp(z)=\left({\pi\over 2\omega_1}\right)^2\left[{-{1\over 3}...
...}^\infty \csc^2\left({{n\omega_2\over n_1}\pi}\right)}\right].
\end{displaymath}](w_478.gif) |
(3) |
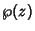 is an Even Function since
is an Even Function since 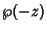 gives the same terms in a different order. To specify
gives the same terms in a different order. To specify 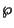 completely, its periods or invariants, written
completely, its periods or invariants, written
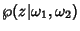 and
and
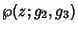 ,
respectively, must also be specified.
,
respectively, must also be specified.
The differential equation from which Weierstraß elliptic functions arise can be found by expanding about the origin the function
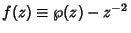 .
.
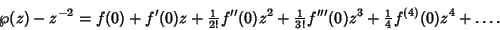 |
(4) |
But 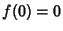 and the function is even, so
and the function is even, so
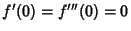 and
and
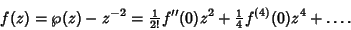 |
(5) |
Taking the derivatives
So
Plugging in,
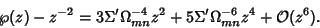 |
(12) |
Define the Invariants
then
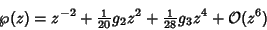 |
(15) |
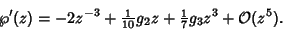 |
(16) |
Now cube (15) and square (16)
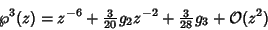 |
(17) |
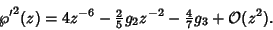 |
(18) |
Taking (18) minus 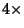 (17) cancels out the
(17) cancels out the 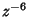 term, giving
term, giving
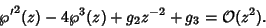 |
(20) |
But, from (5)
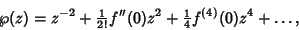 |
(21) |
so
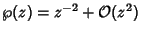 and (20) can be written
and (20) can be written
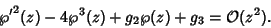 |
(22) |
The Weierstraß elliptic function is analytic at the origin and therefore at all points congruent to the origin.
There are no other places where a singularity can occur, so this function is an Elliptic Function with no
Singularities. By Liouville's Elliptic Function Theorem, it is therefore a constant. But
as 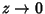 ,
,
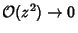 , so
, so
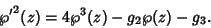 |
(23) |
The solution to the differential equation
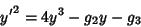 |
(24) |
is therefore given by
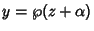 , providing that numbers
, providing that numbers 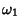 and
and 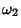 exist which satisfy the equations
defining the Invariants. Writing the differential equation in terms of its roots
exist which satisfy the equations
defining the Invariants. Writing the differential equation in terms of its roots
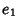 ,
, 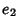 , and
, and 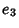 ,
,
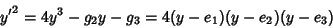 |
(25) |
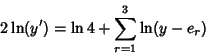 |
(26) |
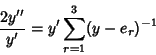 |
(27) |
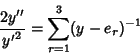 |
(28) |
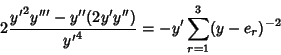 |
(29) |
 |
(30) |
Now take (30) divided by 4 plus [(30) divided by 4] quantity squared,
![\begin{displaymath}
\left({{y'''\over 2{y'}^3}-{{y''}^2\over {y'}^4}}\right)+\le...
...{-2} +{1\over 16} \left[{\,\sum_{r=1}^3 (y-e_r)^{-1}}\right]^2
\end{displaymath}](w_534.gif) |
(31) |
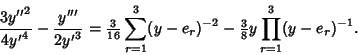 |
(32) |
The term on the right is half the Schwarzian Derivative.
The Derivative of the Weierstraß elliptic function is given by
This is an Odd Function which is itself an elliptic function with pole of order 3 at  . The Integral is
given by
. The Integral is
given by
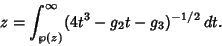 |
(34) |
A duplication formula is obtained as follows.
A general addition theorem is obtained as follows. Given
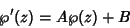 |
(36) |
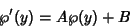 |
(37) |
with zero 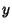 and
and 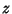 where
where
 , find the third zero
, find the third zero 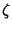 . Consider
. Consider
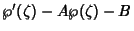 . This has a pole of order three at
. This has a pole of order three at 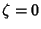 , but the sum of zeros (
, but the sum of zeros (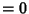 ) equals the sum of
poles for an Elliptic Function, so
) equals the sum of
poles for an Elliptic Function, so 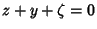 and
and 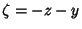 .
.
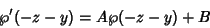 |
(38) |
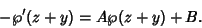 |
(39) |
Combining (36), (37), and (39) gives
![\begin{displaymath}
\left[{\matrix{\wp(z) & \wp'(z) & 1\cr \wp(y) & \wp'(y) & 1\...
... -1\cr B\cr}}\right] = \left[{\matrix{0\cr 0\cr 0\cr}}\right],
\end{displaymath}](w_557.gif) |
(40) |
so
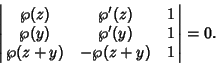 |
(41) |
Defining 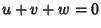 where
where 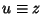 and
and 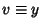 gives the symmetric form
gives the symmetric form
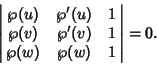 |
(42) |
To get the expression explicitly, start again with
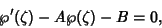 |
(43) |
where
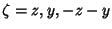 .
.
![\begin{displaymath}
{\wp'}^2(\zeta)-[A\wp(\zeta)+B]^2=0.
\end{displaymath}](w_565.gif) |
(44) |
But
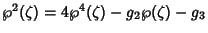 , so
, so
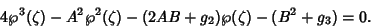 |
(45) |
The solutions
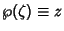 are given by
are given by
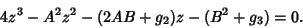 |
(46) |
But the sum of roots equals the Coefficient of the squared term, so
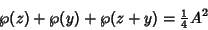 |
(47) |
![\begin{displaymath}
\wp'(z)-\wp'(y)=A[\wp(z)-\wp(y)]
\end{displaymath}](w_571.gif) |
(48) |
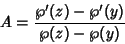 |
(49) |
![\begin{displaymath}
\wp(z+y)={1\over 4}\left[{\wp(z)-\wp'(y)\over \wp(z)-\wp(y)}\right]^2-\wp(z)-\wp(y).
\end{displaymath}](w_573.gif) |
(50) |
Half-period identities include
Multiplying through,
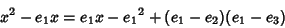 |
(52) |
![\begin{displaymath}
x^2-2e_1+[{e_1}^2-(e_1-e_2)(e_1-e_3)]=0,
\end{displaymath}](w_578.gif) |
(53) |
which gives
From Whittaker and Watson (1990, p. 445),
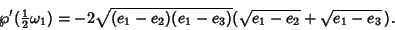 |
(55) |
The function is Homogeneous,
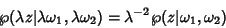 |
(56) |
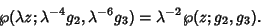 |
(57) |
To invert the function, find 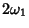 and
and 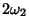 of
of
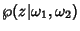 when given
when given
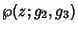 . Let
. Let
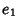 ,
, 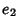 , and
, and 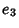 be the roots such that
be the roots such that
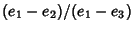 is not a Real Number
is not a Real Number 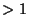 or
or 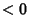 . Determine
the Parameter
. Determine
the Parameter 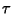 from
from
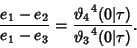 |
(58) |
Now pick
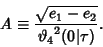 |
(59) |
As long as
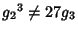 , the periods are then
, the periods are then
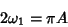 |
(60) |
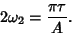 |
(61) |
Weierstraß elliptic functions can be expressed in terms of Jacobi Elliptic Functions by
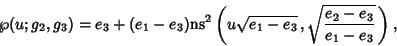 |
(62) |
where
and the Invariants are
Here,
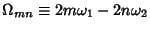 .
.
An addition formula for the Weierstraß elliptic function can be derived as follows.
![\begin{displaymath}
\wp(z+\omega_1)+\wp(z)+\wp(\omega_1) = {1\over 4} \left[{\wp...
...a_1)}\right]^2 = {1\over 4} {{\wp'}^2(z)\over [\wp(z)-e_1]^2}.
\end{displaymath}](w_604.gif) |
(68) |
Use
![\begin{displaymath}
\wp'(z)=4\prod_{r=1}^3 [\wp(z)-e_r],
\end{displaymath}](w_605.gif) |
(69) |
so
Use
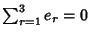 ,
,
But
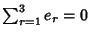 and
and
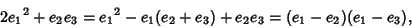 |
(72) |
so
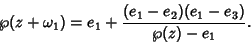 |
(73) |
The periods of the Weierstraß elliptic function are given as follows. When 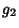 and
and 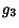 are Real and
are Real and
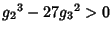 , then
, then 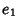 ,
, 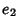 , and
, and 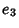 are Real and defined such that
are Real and defined such that
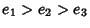 .
.
The roots of the Weierstraß elliptic function satisfy
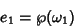 |
(77) |
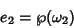 |
(78) |
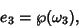 |
(79) |
where
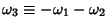 . The
. The 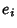 s are Roots of
s are Roots of 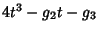 and are unequal so that
and are unequal so that
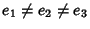 . They can be found from the relationships
. They can be found from the relationships
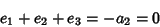 |
(80) |
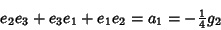 |
(81) |
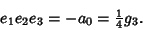 |
(82) |
See also Equianharmonic Case, Lemniscate Case, Pseudolemniscate Case
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Weierstrass Elliptic and Related Functions.'' Ch. 18 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 627-671, 1972.
Fischer, G. (Ed.). Plates 129-131 in
Mathematische Modelle/Mathematical Models, Bildband/Photograph Volume.
Braunschweig, Germany: Vieweg, pp. 126-128, 1986.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England:
Cambridge University Press, 1990.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() . The above plots show the Weierstraß elliptic function
. The above plots show the Weierstraß elliptic function ![]() and its derivative
and its derivative
![]() for invariants (defined below) of
for invariants (defined below) of ![]() and
and ![]() . Weierstraß elliptic functions are denoted
. Weierstraß elliptic functions are denoted ![]() and
can be defined by
and
can be defined by
![\begin{displaymath}
\wp(z) = {1\over z^2} + \setbox0=\hbox{$\scriptstyle{m, n=-\...
...a_1-2n\omega_2)^2}-{1\over (2m\omega_1+2n\omega_2)^2}}\right].
\end{displaymath}](w_475.gif)
![\begin{displaymath}
\wp(z)=\left({\pi\over 2\omega_1}\right)^2\left[{-{1\over 3}...
...}^\infty \csc^2\left({{n\omega_2\over n_1}\pi}\right)}\right].
\end{displaymath}](w_478.gif)
![]() .
.
![]() ,
,
![]() , so
, so
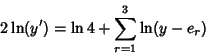
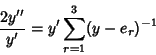
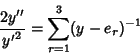
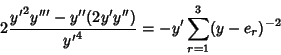

![\begin{displaymath}
\left({{y'''\over 2{y'}^3}-{{y''}^2\over {y'}^4}}\right)+\le...
...{-2} +{1\over 16} \left[{\,\sum_{r=1}^3 (y-e_r)^{-1}}\right]^2
\end{displaymath}](w_534.gif)
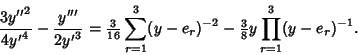
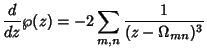
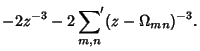
![$\displaystyle \lim_{y\to z} \wp(y+z) ={1\over 4} \lim_{y\to z} \left[{\wp'(z)-\wp'(y)\over \wp(z)-\wp(y)}\right]^2-\wp(z)-\lim_{y\to z} \wp(y)$](w_541.gif)
![$\displaystyle {1\over 4}\lim_{h\to 0} \left[{\wp(z)-\wp'(z+h)\over \wp(z)-\wp(z+h)}\right]^2-2\wp(z)$](w_542.gif)
![$\displaystyle {1\over 4}\left\{{\left[{\lim_{h\to 0} {\wp'(z)-\wp'(z+h)\over h}}\right]\left[{\lim_{h\to 0} {h\over \wp(z)-\wp(z+h)}}\right]}\right\}^2-2\wp(z)$](w_543.gif)
![$\displaystyle {1\over 4}\left[{\wp''(z)\over\wp'(z)}\right]^2-2\wp(z)$](w_544.gif)
![\begin{displaymath}
\left[{\matrix{\wp(z) & \wp'(z) & 1\cr \wp(y) & \wp'(y) & 1\...
... -1\cr B\cr}}\right] = \left[{\matrix{0\cr 0\cr 0\cr}}\right],
\end{displaymath}](w_557.gif)
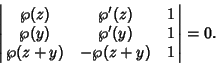
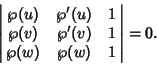
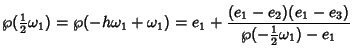
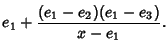
![]() and
and ![]() of
of
![]() when given
when given
![]() . Let
. Let
![]() ,
, ![]() , and
, and ![]() be the roots such that
be the roots such that
![]() is not a Real Number
is not a Real Number ![]() or
or ![]() . Determine
the Parameter
. Determine
the Parameter ![]() from
from
![\begin{displaymath}
\wp'(z)=4\prod_{r=1}^3 [\wp(z)-e_r],
\end{displaymath}](w_605.gif)
![$\displaystyle -\wp(z)-e_1+{1\over 4} {4\prod_{r=1}^3 [\wp(z)-e_r]\over [\wp(z)-e_1]^2}$](w_607.gif)
![$\displaystyle -\wp(z)-e_1+{[\wp(z)-e_2][\wp(z)-e_3]\over \wp(z)-e_1}.$](w_608.gif)
![$\displaystyle e_1+{[-2e_1-\wp(z)][\wp(z)-e_1]\over \wp(z)-e_1}+ {\wp^2(z)-\wp(z)(e_2+e_3)+e_2e_3\over \wp(z)-e_1}$](w_610.gif)
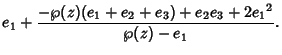
![]() and
and ![]() are Real and
are Real and
![]() , then
, then ![]() ,
, ![]() , and
, and ![]() are Real and defined such that
are Real and defined such that
![]() .
.