Tau-Dirichlet Series

$$\tau_{DS}(z) \equiv \sum_{n=1}^\infty {\tau(n)\over n^z},$$

where $\tau(n)$ is the Tau Function. Ramanujan conjectured that all nontrivial zeros of $\tau_{DS}(S)$ lie on the line $\Re[z]=6$.

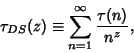
See also Tau Function

References

Spira, R. ``Calculation of the Ramanujan Tau-Dirichlet Series.'' Math. Comput. 27, 379-385, 1973.

Yoshida, H. ``On Calculations of Zeros of L-Functions Related with Ramanujan's Discriminant Function on the Critical Line.'' J. Ramanujan Math. Soc. 3, 87-95, 1988.