|
|
|
The number of representations of ![]() by
by ![]() squares is denoted
squares is denoted ![]() . The Mathematica
. The Mathematica
![]() (Wolfram Research,
Champaign, IL) function NumberTheory`NumberTheoryFunctions`SumOfSquaresR[k,n] gives
(Wolfram Research,
Champaign, IL) function NumberTheory`NumberTheoryFunctions`SumOfSquaresR[k,n] gives ![]() .
.
![]() is often simply written
is often simply written ![]() . Jacobi
. Jacobi ![]() solved the problem for
solved the problem for ![]() , 4, 6, and 8. The first cases
, 4, 6, and 8. The first cases ![]() ,
4, and 6 were found by equating Coefficients of the Theta Function
,
4, and 6 were found by equating Coefficients of the Theta Function
![]() ,
,
![]() , and
, and
![]() . The solutions for
. The solutions for ![]() and 12 were found by Liouville and Eisenstein, and
Glaisher (1907) gives a table of
and 12 were found by Liouville and Eisenstein, and
Glaisher (1907) gives a table of ![]() for
for ![]() .
. ![]() was found as a finite sum involving quadratic reciprocity
symbols by Dirichlet.
was found as a finite sum involving quadratic reciprocity
symbols by Dirichlet. ![]() and
and ![]() were found by Eisenstein, Smith, and Minkowski.
were found by Eisenstein, Smith, and Minkowski.
![]() is 0 whenever
is 0 whenever ![]() has a Prime divisor of the form
has a Prime divisor of the form ![]() to an Odd Power; it doubles upon
reaching a new Prime of the form
to an Odd Power; it doubles upon
reaching a new Prime of the form ![]() . It is given explicitly by
. It is given explicitly by
| (1) |
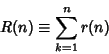 |
(2) |
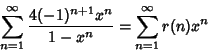 |
(3) |
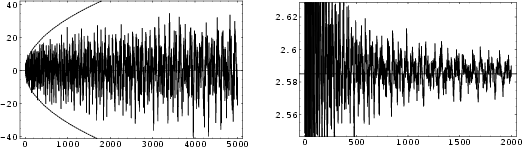
Asymptotic results include
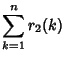 |
(4) | ||
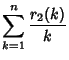 |
(5) |
![\begin{displaymath}
\left[{\sum_{k=1}^n r_2(k)}\right]-\pi n,
\end{displaymath}](r_33.gif) |
(6) |
![\begin{displaymath}
\left[{\sum_{k=1}^n {r_2(k)\over k}}\right]-\pi\ln n,
\end{displaymath}](r_35.gif) |
(7) |
The number of solutions of
| (8) |
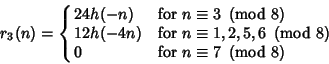 |
(9) |
Additional higher-order identities are given by
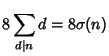 |
(10) | ||
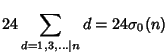 |
(11) | ||
| (12) | |||
| (13) |
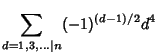 |
(14) | ||
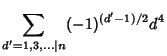 |
(15) | ||
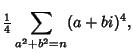 |
(16) |
Similar expressions exist for larger Even ![]() , but they quickly become extremely complicated and can be written simply only
in terms of expansions of modular functions.
, but they quickly become extremely complicated and can be written simply only
in terms of expansions of modular functions.
See also Class Number, Landau-Ramanujan Constant, Prime Factors, Sierpinski Constant, Tau Function
References
Arno, S. ``The Imaginary Quadratic Fields of Class Number 4.'' Acta Arith. 60, 321-334, 1992.
Boulyguine. Comptes Rendus Paris 161, 28-30, 1915.
New York: Chelsea, p. 317, 1952.
Glaisher, J. W. L. ``On the Numbers of a Representation of a Number as a Sum of
Grosswald, E. Representations of Integers as Sums of Squares. New York: Springer-Verlag, 1985.
Hardy, G. H. ``The Representation of Numbers as Sums of Squares.'' Ch. 9 in
Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1959.
Hardy, G. H. and Wright, E. M. ``The Function
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 162-153, 1993.
Sloane, N. J. A. Sequences
A014198 and
A004018/M3218
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
![]() Squares, where
Squares, where ![]() Does Not Exceed 18.''
Proc. London Math. Soc. 5, 479-490, 1907.
Does Not Exceed 18.''
Proc. London Math. Soc. 5, 479-490, 1907.
![]() ,'' ``Proof of the Formula for
,'' ``Proof of the Formula for ![]() ,'' ``The Generating Function of
,'' ``The Generating Function of ![]() ,''
and ``The Order of
,''
and ``The Order of ![]() .'' §16.9, 16.10, 17.9, and 18.7 in An Introduction to the Theory of Numbers, 5th ed.
Oxford, England: Clarendon Press, pp. 241-243, 256-258, and 270-271, 1979.
.'' §16.9, 16.10, 17.9, and 18.7 in An Introduction to the Theory of Numbers, 5th ed.
Oxford, England: Clarendon Press, pp. 241-243, 256-258, and 270-271, 1979.
|
|
|
© 1996-9 Eric W. Weisstein