|
|
|
N.B. A detailed on-line essay by S. Finch was the starting point for this entry.
Let ![]() denote the number of Positive Integers not exceeding
denote the number of Positive Integers not exceeding ![]() which can be expressed as a sum of
two squares, then
which can be expressed as a sum of
two squares, then
| (1) |
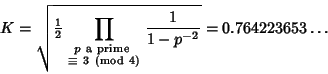 |
(2) |
![\begin{displaymath}
K={1\over\sqrt{2}}\prod_{n=1}^\infty\left[{\left({1-{1\over 2^{2^n}}}\right){\zeta(2^n)\over\beta(2^n)}}\right]^{1/(2^n+1)},
\end{displaymath}](l1_521.gif) |
(3) |
| (4) |
| (5) |
![$\displaystyle {1\over 2}\left[{1-\ln\left({\pi e^\gamma\over L}\right)}\right]-...
...le p{\rm\ prime}\atop\scriptstyle p=4k+3}{1\over p^{-2s}}}\right)}\right]_{s=1}$](l1_526.gif) |
|||
| (6) |
| (7) |
References
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 60-66, 1994.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/lr/lr.html
Flajolet, P. and Vardi, I. ``Zeta Function Expansions of Classical Constants.'' Unpublished manuscript. 1996.
http://pauillac.inria.fr/algo/flajolet/Publications/landau.ps.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea,
pp. 61-63, 1940.
Landau, E. ``Über die Einteilung der positiven ganzen Zahlen in vier Klassen nach der Mindeszahl der zu ihrer
additiven Zusammensetzung erforderlichen Quadrate.'' Arch. Math. Phys. 13, 305-312, 1908.
Shanks, D. ``The Second-Order Term in the Asymptotic Expansion of
Shanks, D. ``Non-Hypotenuse Numbers.'' Fibonacci Quart. 13, 319-321, 1975.
Shanks, D. and Schmid, L. P. ``Variations on a Theorem of Landau. I.'' Math. Comput. 20, 551-569, 1966.
Shiu, P. ``Counting Sums of Two Squares: The Meissel-Lehmer Method.'' Math. Comput. 47, 351-360, 1986.
![]() .'' Math. Comput. 18, 75-86, 1964.
.'' Math. Comput. 18, 75-86, 1964.
|
|
|
© 1996-9 Eric W. Weisstein