Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/lk/lk.html
Franco, Z. M.; Kaper, H. G.; Kwong, M. N.; and Zettl, A. ``Bounds for the Best Constants in Landau's Inequality on the
Line.'' Proc. Roy. Soc. Edinburgh 95A, 257-262, 1983.
Franco, Z. M.; Kaper, H. G.; Kwong, M. N.; and Zettl, A. ``Best Constants in Norm Inequalities for Derivatives on a
Half Line.'' Proc. Roy. Soc. Edinburgh 100A, 67-84, 1985.
Hardy, G. H.; Littlewood, J. E.; and Pólya, G. Inequalities. Cambridge, England: Cambridge University Press, 1934.
Kolmogorov, A. ``On Inequalities Between the Upper Bounds of the Successive Derivatives of an Arbitrary Function on an Infinite Integral.''
Amer. Math. Soc. Translations, Ser. 1 2, 233-243, 1962.
Kupcov, N. P. ``Kolmogorov Estimates for Derivatives in 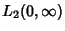 .'' Proc. Steklov Inst. Math. 138, 101-125, 1975.
.'' Proc. Steklov Inst. Math. 138, 101-125, 1975.
Kwong, M. K. and Zettl, A. Norm Inequalities for Derivatives and Differences. New York: Springer-Verlag, 1992.
Landau, E. ``Einige Ungleichungen für zweimal differentzierbare Funktionen.'' Proc. London Math. Soc. Ser. 2 13,
43-49, 1913.
Landau, E. ``Die Ungleichungen für zweimal differentzierbare Funktionen.'' Danske Vid. Selsk. Math. Fys. Medd. 6, 1-49,
1925.
Ljubic, J. I. ``On Inequalities Between the Powers of a Linear Operator.'' Amer. Math. Soc. Trans. Ser. 2
40, 39-84, 1964.
Neta, B. ``On Determinations of Best Possible Constants in Integral Inequalities Involving Derivatives.'' Math. Comput. 35,
1191-1193, 1980.
Schoenberg, I. J. ``The Elementary Case of Landau's Problem of Inequalities Between Derivatives.'' Amer. Math. Monthly 80,
121-158, 1973.
![]() be the Supremum of
be the Supremum of ![]() , a real-valued function
, a real-valued function ![]() defined on
defined on ![]() . If
. If ![]() is twice
differentiable and both
is twice
differentiable and both ![]() and
and ![]() are bounded, Landau (1913) showed that
are bounded, Landau (1913) showed that
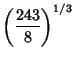
![]() be the Supremum of
be the Supremum of ![]() , a real-valued function
, a real-valued function ![]() defined on
defined on
![]() . If
. If ![]() is
twice differentiable and both
is
twice differentiable and both ![]() and
and ![]() are bounded, Hadamard (1914) showed that
are bounded, Hadamard (1914) showed that
![\begin{displaymath}
a_n={4\over\pi} \sum_{j=0}^\infty \left[{(-1)^j\over 2j+1}\right]^{n+1}
\end{displaymath}](l1_483.gif)
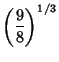
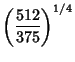
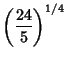
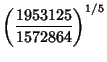
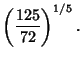
![]() defined on
defined on
![]() , define
, define
![\begin{displaymath}
\vert\vert f\vert\vert=\sqrt{\int_{-\infty}^\infty [f(x)]^2\,dx}\,.
\end{displaymath}](l1_494.gif)
![]() defined on
defined on ![]() , define
, define
![\begin{displaymath}
\vert\vert f\vert\vert=\sqrt{\int_0^\infty [f(x)]^2\,dx}.
\end{displaymath}](l1_498.gif)
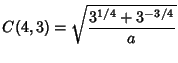
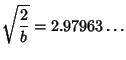
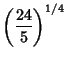
![]() , 2,
, 2, ![]() are the only ones for which the best constants have exact expressions (Kwong and Zettl 1992,
Franco et al. 1983).
are the only ones for which the best constants have exact expressions (Kwong and Zettl 1992,
Franco et al. 1983).
![]() .'' Proc. Steklov Inst. Math. 138, 101-125, 1975.
.'' Proc. Steklov Inst. Math. 138, 101-125, 1975.