|
|
|
A series of the form
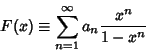 |
(1) |
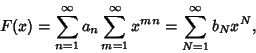 |
(2) |
| (3) |
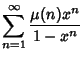 |
(4) | ||
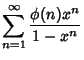 |
(5) | ||
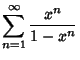 |
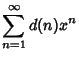 |
(6) | |
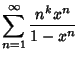 |
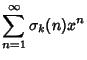 |
(7) | |
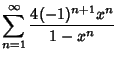 |
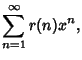 |
(8) |
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Number Theoretic Functions.'' §24.3.1 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 826-827, 1972.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed.
Oxford, England: Clarendon Press, pp. 257-258, 1979.