|
|
|
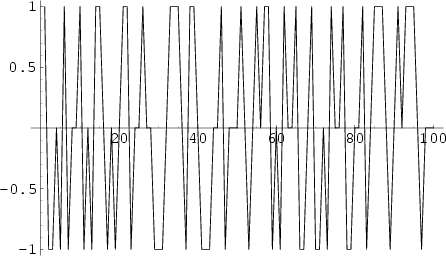

The Summatory Function of the Möbius function is called Mertens Function.
See also Braun's Conjecture, Mertens Function, Möbius Inversion Formula, Möbius Periodic Function, Prime Zeta Function, Riemann Function, Squarefree
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``The Möbius Function.'' §24.3.1 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 826, 1972.
Deléglise, M. and Rivat, J. ``Computing the Summation of the Möbius Function.'' Experiment. Math. 5, 291-295, 1996.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford: Clarendon Press, p. 236, 1979.
Sloane, N. J. A. Sequence
A008683
in ``The On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
Vardi, I. Computational Recreations in Mathematica. Redwood City, CA: Addison-Wesley, pp. 7-8 and 223-225, 1991.