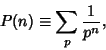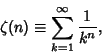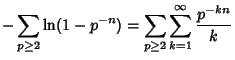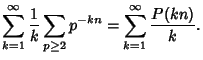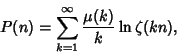Prime Zeta Function

The prime zeta function

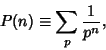$$P(n)\equiv \sum_p {1\over p^n},$$ (1)

where the sum is taken over Primes is a generalization of the Riemann Zeta Function

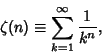$$\zeta(n)\equiv \sum_{k=1}^\infty {1\over k^n},$$ (2)

where the sum is over all integers. The prime zeta function can be expressed in terms of the Riemann Zeta Function by

$$\ln\zeta(n) = -\sum_{p\geq 2}\ln(1-p^{-n}) = \sum_{p\geq 2} \sum_{k=1}^\infty {p^{-kn}\over k}$$

$$= \sum_{k=1}^\infty {1\over k} \sum_{p\geq 2} p^{-kn}=\sum_{k=1}^\infty {P(kn)\over k}.$$ (3)

Inverting then gives

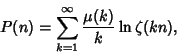$$P(n)=\sum_{k=1}^\infty {\mu(k)\over k}\ln\zeta(kn),$$ (4)

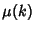where $\mu(k)$ is the Möbius Function. The values for the first few integers starting with two are

$$P(2) \approx 0.452247$$ (5)

$$P(3) \approx 0.174763$$ (6)

$$P(4) \approx 0.0769931$$ (7)

$$P(5) \approx 0.035755.$$ (8)

See also Möbius Function, Riemann Zeta Function, Zeta Function

References

Hardy, G. H. and Weight, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Oxford University Press, pp. 355-356, 1979.