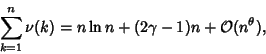Let
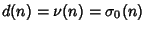 be the number of Divisors of
be the number of Divisors of  (including
(including  itself). For a Prime
itself). For a Prime
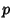 ,
, 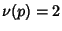 . In general,
. In general,
where 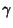 is the Euler-Mascheroni Constant. Dirichlet
is the Euler-Mascheroni Constant. Dirichlet  originally gave
originally gave
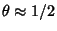 .
As of 1988, this had been reduced to
.
As of 1988, this had been reduced to
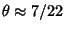 .
.
See also Divisor Function
© 1996-9 Eric W. Weisstein
1999-05-24
![]() be the number of Divisors of
be the number of Divisors of ![]() (including
(including ![]() itself). For a Prime
itself). For a Prime
![]() ,
, ![]() . In general,
. In general,