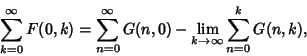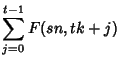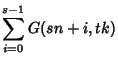A pair of Closed Form functions 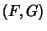 is said to be a Wilf-Zeilberger pair if
is said to be a Wilf-Zeilberger pair if
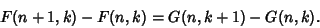 |
(1) |
The Wilf-Zeilberger formalism provides succinct proofs of known identities and allows new identities to be discovered
whenever it succeeds in finding a proof certificate for a known identity. However, if the starting point is an unknown
hypergeometric sum, then the Wilf-Zeilberger method cannot discover a closed form solution, while Zeilberger's
Algorithm can.
Wilf-Zeilberger pairs are very useful in proving Hypergeometric Identities of the form
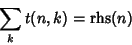 |
(2) |
for which the Summand 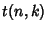 vanishes for all
vanishes for all 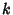 outside some finite interval. Now divide by the right-hand side to obtain
outside some finite interval. Now divide by the right-hand side to obtain
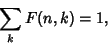 |
(3) |
where
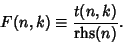 |
(4) |
Now use a Rational Function 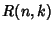 provided by Zeilberger's Algorithm, define
provided by Zeilberger's Algorithm, define
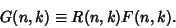 |
(5) |
The identity (1) then results. Summing the relation over all integers then telescopes the right side to 0, giving
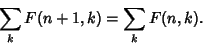 |
(6) |
Therefore, 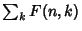 is independent of
is independent of 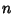 , and so must be a constant. If
, and so must be a constant. If 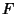 is properly normalized, then
it will be true that
is properly normalized, then
it will be true that
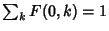 .
.
For example, consider the Binomial Coefficient identity
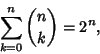 |
(7) |
the function 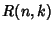 returned by Zeilberger's Algorithm is
returned by Zeilberger's Algorithm is
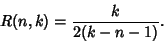 |
(8) |
Therefore,
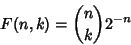 |
(9) |
and
Taking
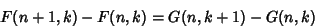 |
(11) |
then gives the alleged identity
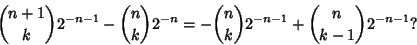 |
(12) |
Expanding and evaluating shows that the identity does actually hold, and it can also be verified that
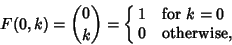 |
(13) |
so
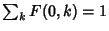 (Petkovsek et al. 1996, pp. 25-27).
(Petkovsek et al. 1996, pp. 25-27).
For any Wilf-Zeilberger pair 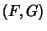 ,
,
![\begin{displaymath}
\sum_{n=0}^\infty G(n,0)=\sum_{n=1}^\infty [F(n,n-1)+G(n-1,n-1)]
\end{displaymath}](w_1013.gif) |
(14) |
whenever either side converges (Zeilberger 1993). In addition,
![$\sum_{n=0}^\infty G(n,0)=\sum_{n=0}^\infty\left[{F(s(n+1),n)+\sum_{i=0}^{s-1} G(sn+i,n)}\right]$](w_1014.gif)
|
|
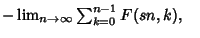
|
(15) |
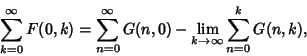 |
(16) |
and
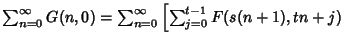
|
|
![$ \left.{+\sum_{i=0}^{s-1}G(sn+i,tn)}\right]-\lim_{n\to\infty}\sum_{k=0}^{n-1} F_{s,t}(n,k),\quad$](w_1018.gif)
|
(17) |
where
(Amdeberhan and Zeilberger 1997). The latter identity has been used to compute Apéry's Constant to a large number of decimal places (Plouffe).
See also Apéry's Constant, Convergence Improvement, Zeilberger's Algorithm
References
Amdeberhan, T. and Zeilberger, D. ``Hypergeometric Series Acceleration via the WZ Method.'' Electronic J. Combinatorics 4, No. 2, R3, 1-3, 1997.
http://www.combinatorics.org/Volume_4/wilftoc.html#R03. Also available at
http://www.math.temple.edu/~zeilberg/mamarim/mamarimhtml/accel.html.
Cipra, B. A. ``How the Grinch Stole Mathematics.'' Science 245, 595, 1989.
Petkovsek, M.; Wilf, H. S.; and Zeilberger, D. ``The WZ Phenomenon.'' Ch. 7 in A=B.
Wellesley, MA: A. K. Peters, pp. 121-140, 1996.
Wilf, H. S. and Zeilberger, D. ``Rational Functions Certify Combinatorial Identities.'' J. Amer. Math. Soc. 3, 147-158, 1990.
Zeilberger, D. ``The Method of Creative Telescoping.'' J. Symb. Comput. 11, 195-204, 1991.
Zeilberger, D. ``Closed Form (Pun Intended!).'' Contemporary Math. 143, 579-607, 1993.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() is said to be a Wilf-Zeilberger pair if
is said to be a Wilf-Zeilberger pair if
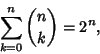
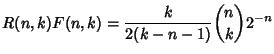
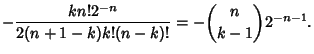
![]() ,
,
![\begin{displaymath}
\sum_{n=0}^\infty G(n,0)=\sum_{n=1}^\infty [F(n,n-1)+G(n-1,n-1)]
\end{displaymath}](w_1013.gif)