Logarithm

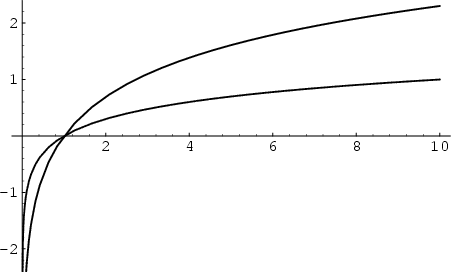
The logarithm is defined to be the Inverse Function of taking a number to a given Power. Therefore, for any $x$ and $b$,

$$x=b^{\log_b x},$$ (1)

or equivalently,

$$x=\log_b(b^x).$$ (2)

Here, the Power $b$ is known as the Base of the logarithm. For any Base, the logarithm function has a Singularity at $x=0$. In the above plot, the solid curve is the logarithm to Base $e$ (the Natural Logarithm), and the dotted curve is the logarithm to Base 10 (Log).

Logarithms are used in many areas of science and engineering in which quantities vary over a large range. For example, the decibel scale for the loudness of sound, the Richter scale of earthquake magnitudes, and the astronomical scale of stellar brightnesses are all logarithmic scales.

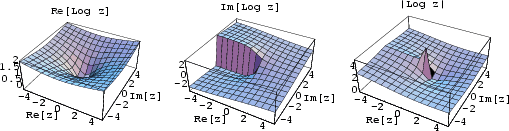
The logarithm can also be defined for Complex arguments, as shown above. If the logarithm is taken as the forward function, the function taking the Base to a given Power is then called the Antilogarithm.

For $x=\log N$, $\left\lfloor{x}\right\rfloor$ is called the Characteristic and $x-\left\lfloor{x}\right\rfloor$ is called the Mantissa. Division and multiplication identities follow from these

$$xy = b^{\log_b x}b^{\log_b y} = b^{\log_b x+\log_b y},$$ (3)

from which it follows that

$$\log_b(xy) = \log_b x+\log_b y$$ (4)

$$\log_b\left({x\over y}\right)= \log_b x-\log_b y$$ (5)

$$\log_b x^n = n \log_b x.$$ (6)

There are a number of properties which can be used to change from one Base to another

$$a = a^{\log_a b/\log_a b} = (a^{\log_a b})^{1/\log_a b} = b^{1/\log_a b}$$ (7)

$$\log_b a = { 1\over \log_a b}$$ (8)

$$\log_x z = \log_x(y^{\log_y z}) = \log_y z\log_x y$$ (9)

$$\log_y z = {\log_x z\over \log_x y}$$ (10)

$$a^x = b^{x/\log_a b} = b^{x \log_b a}.$$ (11)

The logarithm Base e is called the Natural Logarithm and is denoted $\ln x$ (Ln). The logarithm Base 10 is denoted $\log x$ (Log), (although mathematics texts often use $\log x$ to mean $\ln x$). The logarithm Base 2 is denoted $\lg x$ (Lg).

An interesting property of logarithms follows from looking for a number $y$ such that

$$\log_b(x+y)=-\log_b(x-y)$$ (12)

$$x+y={1\over x-y}$$ (13)

$$x^2-y^2=1$$ (14)

$$y=\sqrt{x^2-1},$$ (15)

so

$$\log_b(x+\sqrt{x^2-1}\,) = -\log_b(x-\sqrt{x^2-1}\,).$$ (16)

Numbers of the form $\log_a b$ are Irrational if $a$ and $b$ are Integers, one of which has a Prime factor which the other lacks. A. Baker made a major step forward in Transcendental Number theory by proving the transcendence of sums of numbers of the form $\alpha\ln\beta$ for $\alpha$ and $\beta$ Algebraic Numbers.

See also Antilogarithm, Cologarithm, e, Exponential Function, Harmonic Logarithm, Lg, Ln, Log, Logarithmic Number, Napierian Logarithm, Natural Logarithm, Power

References

Abramowitz, M. and Stegun, C. A. (Eds.). ``Logarithmic Function.'' §4.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 67-69, 1972.

Conway, J. H. and Guy, R. K. ``Logarithms.'' The Book of Numbers. New York: Springer-Verlag, pp. 248-252, 1996.

Beyer, W. H. ``Logarithms.'' CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 159-160, 1987.

Pappas, T. ``Earthquakes and Logarithms.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 20-21, 1989.

Spanier, J. and Oldham, K. B. ``The Logarithmic Function $\ln(x)$.'' Ch. 25 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 225-232, 1987.