|
|
|
The Logarithm having base e, where
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
The Mercator Series
| (6) |
Continued Fraction representations of logarithmic functions include
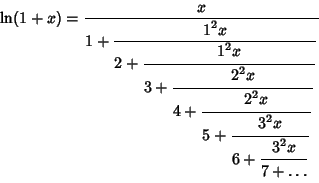 |
(7) |
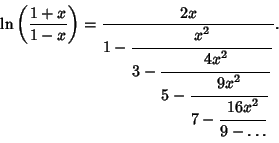 |
(8) |
For a Complex Number ![]() , the natural logarithm satisfies
, the natural logarithm satisfies
| (9) |
| (10) |
Some special values of the natural logarithm are
| (11) |
| (12) |
| (13) |
| (14) |
An identity for the natural logarithm of 2 discovered using the PSLQ Algorithm is
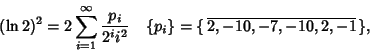 |
(15) |
See also e, Jensen's Formula, Lg, Logarithm
References
Bailey, D.; Borwein, P.; and Plouffe, S. ``On the Rapid Computation of Various Polylogarithmic Constants.''
http://www.cecm.sfu.ca/~pborwein/PAPERS/P123.ps.
Bailey, D. and Plouffe, S. ``Recognizing Numerical Constants.''
http://www.cecm.sfu.ca/organics/papers/bailey/.
|
|
|
© 1996-9 Eric W. Weisstein