|
|
|
A Real Number ![]() whose Continued Fraction is periodic, and the periodic sequence of terms is
composed of a string of 1s followed by an Integer
whose Continued Fraction is periodic, and the periodic sequence of terms is
composed of a string of 1s followed by an Integer ![]() ,
,
![\begin{displaymath}
\nu =[\,\overline{\underbrace{1, 1, \ldots, 1}_P, n}\,].
\end{displaymath}](n_143.gif) |
(1) |
![\begin{displaymath}
\nu = [\underbrace{1, 1, \ldots, 1}_P, n, \nu^{-1}],
\end{displaymath}](n_144.gif) |
(2) |
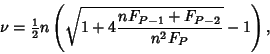 |
(3) |
| (4) |
See also Noble Number
References
Schroeder, M. R.
Number Theory in Science and Communication: With Applications in Cryptography, Physics, Digital Information, Computing, and Self-Similarity, 2nd enl. ed., corr. printing.
Berlin: Springer-Verlag, 1990.
Schroeder, M. ``Noble and Near Noble Numbers.'' In Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise.
New York: W. H. Freeman, pp. 392-394, 1991.