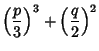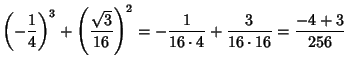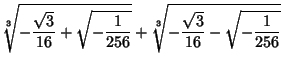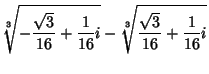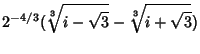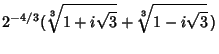Trigonometric functions of 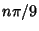 radians for
radians for  an integer not divisible by 3 (e.g., 40° and 80°) cannot
be expressed in terms of sums, products, and finite root extractions on real rational numbers because 9 is not a
product of distinct Fermat Primes. This also means that the Nonagon is not a
Constructible Polygon.
an integer not divisible by 3 (e.g., 40° and 80°) cannot
be expressed in terms of sums, products, and finite root extractions on real rational numbers because 9 is not a
product of distinct Fermat Primes. This also means that the Nonagon is not a
Constructible Polygon.
However, exact expressions involving roots of complex numbers can still be derived using the trigonometric identity
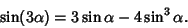 |
(1) |
Let
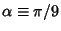 and
and
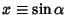 . Then the above identity gives the Cubic Equation
. Then the above identity gives the Cubic Equation
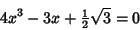 |
(2) |
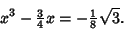 |
(3) |
This cubic is of the form
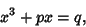 |
(4) |
where
The Discriminant is then
There are therefore three Real distinct roots, which are approximately
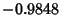 , 0.3240, and 0.6428. We want the one in the first Quadrant, which is 0.3240.
, 0.3240, and 0.6428. We want the one in the first Quadrant, which is 0.3240.
Similarly,
Because of the Newton's Relations, we have the identities
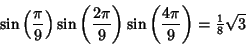 |
(10) |
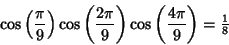 |
(11) |
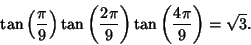 |
(12) |
See also Nonagon, Star of Goliath
© 1996-9 Eric W. Weisstein
1999-05-26
![]() radians for
radians for ![]() an integer not divisible by 3 (e.g., 40° and 80°) cannot
be expressed in terms of sums, products, and finite root extractions on real rational numbers because 9 is not a
product of distinct Fermat Primes. This also means that the Nonagon is not a
Constructible Polygon.
an integer not divisible by 3 (e.g., 40° and 80°) cannot
be expressed in terms of sums, products, and finite root extractions on real rational numbers because 9 is not a
product of distinct Fermat Primes. This also means that the Nonagon is not a
Constructible Polygon.