|
|
|
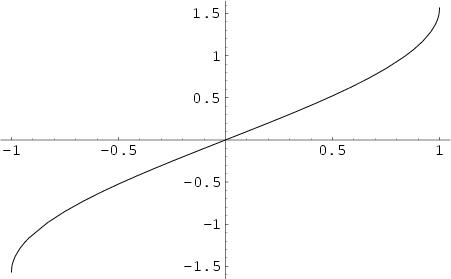
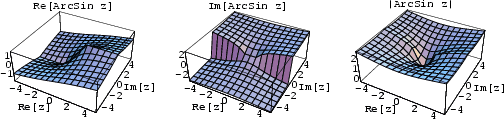
The function ![]() , where
, where ![]() is the Sine and the superscript
is the Sine and the superscript ![]() denotes the Inverse
Function, not the multiplicative inverse. The inverse sine satisfies
denotes the Inverse
Function, not the multiplicative inverse. The inverse sine satisfies
| (1) |
| (2) |
| (3) | |||
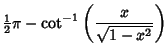 |
(4) | ||
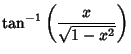 |
(5) |
| (6) | |||
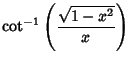 |
(7) | ||
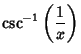 |
(8) | ||
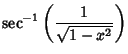 |
(9) |
See also Inverse Cosine, Sine
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Inverse Circular Functions.'' §4.4 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 79-83, 1972.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 142-143, 1987.