Given a Right Triangle with angles defined to be 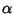 and
and 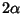 , it must be true that
, it must be true that
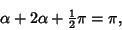 |
(1) |
so
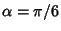 . Define the hypotenuse to have length
. Define the hypotenuse to have length 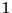 and the side opposite
and the side opposite 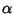 to have length
to have length 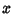 , then the
side opposite
, then the
side opposite 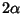 has length
has length 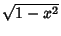 . This gives
. This gives
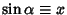 and
and
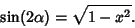 |
(2) |
But
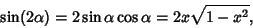 |
(3) |
so we have
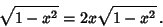 |
(4) |
This gives 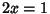 , or
, or
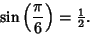 |
(5) |
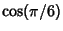 is then computed from
is then computed from
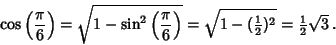 |
(6) |
Summarizing,
See also Hexagon, Hexagram
© 1996-9 Eric W. Weisstein
1999-05-26
![]() and
and ![]() , it must be true that
, it must be true that