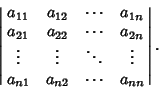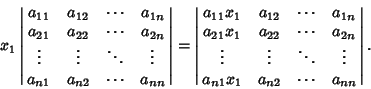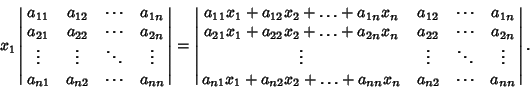Nonhomogeneous matrix equations of the form
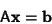 |
(1) |
can be solved by taking the Matrix Inverse to obtain
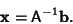 |
(2) |
This equation will have a nontrivial solution Iff the Determinant
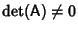 . In general,
more numerically stable techniques of solving the equation include Gaussian Elimination, LU Decomposition, or the
Square Root Method.
. In general,
more numerically stable techniques of solving the equation include Gaussian Elimination, LU Decomposition, or the
Square Root Method.
For a homogeneous 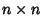 Matrix equation
Matrix equation
![\begin{displaymath}
\left[{\matrix{
a_{11} & a_{12} & \cdots & a_{1n}\cr
a_{21...
...\cr}}\right]
=\left[{\matrix{0\cr 0\cr \vdots\cr 0\cr}}\right]
\end{displaymath}](m_605.gif) |
(3) |
to be solved for the 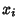 s, consider the Determinant
s, consider the Determinant
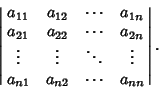 |
(4) |
Now multiply by 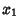 , which is equivalent to multiplying the first column (or any column) by
, which is equivalent to multiplying the first column (or any column) by 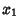 ,
,
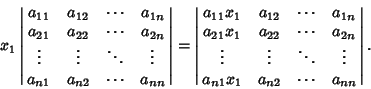 |
(5) |
The value of the Determinant is unchanged if multiples of columns are added to other columns. So add 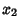 times
column 2, ..., and
times
column 2, ..., and 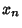 times column
times column 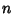 to the first column to obtain
to the first column to obtain
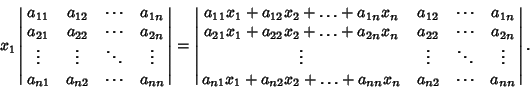 |
(6) |
But from the original Matrix, each of the entries in the first columns is zero since
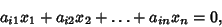 |
(7) |
so
 |
(8) |
Therefore, if there is an 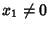 which is a solution, the Determinant is zero. This is also true for
which is a solution, the Determinant is zero. This is also true for 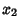 ,
...,
,
..., 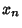 , so the original homogeneous system has a nontrivial solution for all
, so the original homogeneous system has a nontrivial solution for all 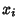 s only if the Determinant is 0.
This approach is the basis for Cramer's Rule.
s only if the Determinant is 0.
This approach is the basis for Cramer's Rule.
Given a numerical solution to a matrix equation, the solution can be iteratively improved using the following
technique. Assume that the numerically obtained solution to
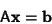 |
(9) |
is
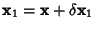 , where
, where
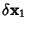 is an error term. The first solution therefore gives
is an error term. The first solution therefore gives
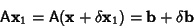 |
(10) |
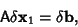 |
(11) |
where 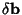 is found by solving (10)
is found by solving (10)
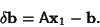 |
(12) |
Combining (11) and (12) then gives
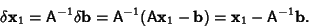 |
(13) |
See also Cramer's Rule, Gaussian Elimination, LU Decomposition, Matrix, Matrix Addition,
Matrix Inverse, Matrix Multiplication, Normal Equation, Square Root Method
© 1996-9 Eric W. Weisstein
1999-05-26
![]() Matrix equation
Matrix equation
![\begin{displaymath}
\left[{\matrix{
a_{11} & a_{12} & \cdots & a_{1n}\cr
a_{21...
...\cr}}\right]
=\left[{\matrix{0\cr 0\cr \vdots\cr 0\cr}}\right]
\end{displaymath}](m_605.gif)