The product
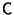 of two Matrices
of two Matrices
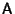 and
and
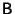 is defined by
is defined by
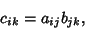 |
(1) |
where 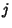 is summed over for all possible values of
is summed over for all possible values of 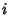 and
and 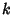 . Therefore, in order for multiplication to be defined, the
dimensions of the Matrices must satisfy
. Therefore, in order for multiplication to be defined, the
dimensions of the Matrices must satisfy
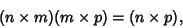 |
(2) |
where 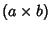 denotes a Matrix with
denotes a Matrix with 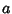 rows and
rows and 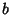 columns. Writing out the product explicitly,
columns. Writing out the product explicitly,
![\begin{displaymath}
\left[{\matrix{c_{11} & c_{12} & \cdots & c_{1p}\cr c_{21} &...
...ots & \vdots\cr b_{m1} & b_{m2} & \cdots & b_{mp}\cr}}\right],
\end{displaymath}](m_640.gif) |
(3) |
where
Matrix multiplication is Associative, as can be seen by taking
![\begin{displaymath}[(ab)c]_{ij} = (ab)_{ik} c_{kj} = (a_{il}b_{lk})c_{kj}.
\end{displaymath}](m_642.gif) |
(4) |
Now, since 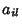 ,
, 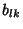 , and
, and 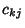 are Scalars, use the Associativity
of Scalar Multiplication to write
are Scalars, use the Associativity
of Scalar Multiplication to write
![\begin{displaymath}
(a_{il}b_{lk})c_{kj} = a_{il}(b_{lk}c_{kj}) = a_{il}(bc)_{lj} = [a(bc)]_{ij}.
\end{displaymath}](m_646.gif) |
(5) |
Since this is true for all 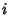 and
and 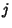 , it must be true that
, it must be true that
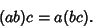 |
(6) |
That is, matrix multiplication is Associative. However, matrix multiplication is not, in general,
Commutative (although it is Commutative if
 and
and
 are Diagonal and
of the same dimension).
are Diagonal and
of the same dimension).
The product of two Block Matrices is given by multiplying each block
![$\left[{\matrix{o & o\cr o & o\cr & & o\cr & & & o & o & o\cr & & & o & o & o\cr...
...x\cr & & x\cr & & & x & x & x\cr & & & x & x & x\cr & & & x & x & x\cr}}\right]$](m_648.gif)
|
|
![$=\left[{\matrix{\left[{\matrix{o & o\cr o & o\cr}}\right]\left[{\matrix{x & x\c...
...\right]\left[{\matrix{x & x & x\cr x & x & x\cr x & x & x\cr}}\right]}}\right].$](m_649.gif)
|
|
|
|
(7) |
See also Matrix, Matrix Addition, Matrix Inverse, Strassen Formulas
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 178-179, 1985.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() of two Matrices
of two Matrices
![]() and
and
![]() is defined by
is defined by
![\begin{displaymath}
\left[{\matrix{c_{11} & c_{12} & \cdots & c_{1p}\cr c_{21} &...
...ots & \vdots\cr b_{m1} & b_{m2} & \cdots & b_{mp}\cr}}\right],
\end{displaymath}](m_640.gif)
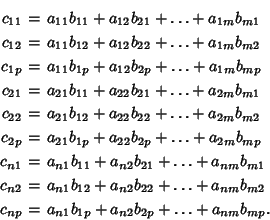
![$\left[{\matrix{o & o\cr o & o\cr & & o\cr & & & o & o & o\cr & & & o & o & o\cr...
...x\cr & & x\cr & & & x & x & x\cr & & & x & x & x\cr & & & x & x & x\cr}}\right]$](m_648.gif)
![$=\left[{\matrix{\left[{\matrix{o & o\cr o & o\cr}}\right]\left[{\matrix{x & x\c...
...\right]\left[{\matrix{x & x & x\cr x & x & x\cr x & x & x\cr}}\right]}}\right].$](m_649.gif)