A diagonal matrix is a Matrix
 of the form
of the form
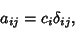 |
(1) |
where 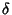 is the Kronecker Delta,
is the Kronecker Delta, 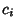 are constants, and there is no summation over indices. The general
diagonal matrix is therefore Square and of the form
are constants, and there is no summation over indices. The general
diagonal matrix is therefore Square and of the form
![\begin{displaymath}
\left[{\matrix{
c_1 & 0 & \cdots & 0\cr
0 & c_2 & \cdots &...
...\vdots & \ddots & \vdots\cr
0 & 0 & \cdots & c_n\cr}}\right].
\end{displaymath}](d1_720.gif) |
(2) |
Given a Matrix equation of the form
![\begin{displaymath}
\left[{\matrix{a_{11} & \cdots & a_{1n}\cr \vdots & \ddots &...
...ots & \ddots & \vdots\cr a_{n1} & \cdots & a_{nn}\cr}}\right],
\end{displaymath}](d1_721.gif) |
(3) |
multiply through to obtain
![\begin{displaymath}
\left[{\matrix{a_{11}\lambda_1 & \cdots & a_{1n}\lambda_n\cr...
...ots\cr a_{n1}\lambda_n & \cdots & a_{nn}\lambda_n\cr}}\right].
\end{displaymath}](d1_722.gif) |
(4) |
Since in general,
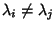 for
for 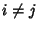 , this can be true only if off-diagonal components vanish.
Therefore, A must be diagonal.
, this can be true only if off-diagonal components vanish.
Therefore, A must be diagonal.
Given a diagonal matrix
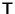 ,
,
![\begin{displaymath}
{\hbox{\sf T}}^n=\left[{\matrix{
t_1 & 0 & \cdots & 0\cr
0...
...ts & \ddots & \vdots\cr
0 & 0 & \cdots & {t_k}^n\cr}}\right].
\end{displaymath}](d1_726.gif) |
(5) |
See also Matrix, Triangular Matrix, Tridiagonal Matrix
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 181-184 and 217-229, 1985.
© 1996-9 Eric W. Weisstein
1999-05-24
![]() of the form
of the form
![\begin{displaymath}
\left[{\matrix{
c_1 & 0 & \cdots & 0\cr
0 & c_2 & \cdots &...
...\vdots & \ddots & \vdots\cr
0 & 0 & \cdots & c_n\cr}}\right].
\end{displaymath}](d1_720.gif)
![\begin{displaymath}
\left[{\matrix{a_{11} & \cdots & a_{1n}\cr \vdots & \ddots &...
...ots & \ddots & \vdots\cr a_{n1} & \cdots & a_{nn}\cr}}\right],
\end{displaymath}](d1_721.gif)
![\begin{displaymath}
\left[{\matrix{a_{11}\lambda_1 & \cdots & a_{1n}\lambda_n\cr...
...ots\cr a_{n1}\lambda_n & \cdots & a_{nn}\lambda_n\cr}}\right].
\end{displaymath}](d1_722.gif)
![]() ,
,
![\begin{displaymath}
{\hbox{\sf T}}^n=\left[{\matrix{
t_1 & 0 & \cdots & 0\cr
0...
...ts & \ddots & \vdots\cr
0 & 0 & \cdots & {t_k}^n\cr}}\right].
\end{displaymath}](d1_726.gif)