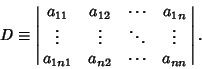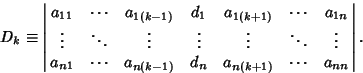Given a set of linear equations
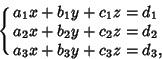 |
(1) |
consider the Determinant
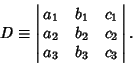 |
(2) |
Now multiply 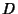 by
by 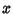 , and use the property of Determinants that Multiplication by a
constant is equivalent to Multiplication of each entry in a given row by that constant
, and use the property of Determinants that Multiplication by a
constant is equivalent to Multiplication of each entry in a given row by that constant
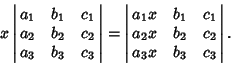 |
(3) |
Another property of Determinants enables us to add a constant times any column to any column and
obtain the same Determinant, so add 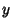 times column 2 and
times column 2 and 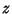 times column 3 to column 1,
times column 3 to column 1,
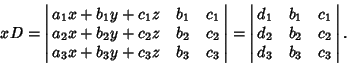 |
(4) |
If
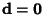 , then (4) reduces to
, then (4) reduces to 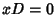 , so the system has nondegenerate solutions (i.e., solutions other than
(0, 0, 0)) only if
, so the system has nondegenerate solutions (i.e., solutions other than
(0, 0, 0)) only if 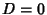 (in which case there is a family of solutions). If
(in which case there is a family of solutions). If
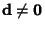 and
and 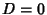 , the
system has no unique solution. If instead
, the
system has no unique solution. If instead
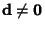 and
and 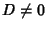 , then solutions are given by
, then solutions are given by
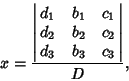 |
(5) |
and similarly for
This procedure can be generalized to a set of 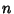 equations so, given a system of
equations so, given a system of 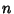 linear equations
linear equations
![\begin{displaymath}
\left[{\matrix{
a_{11} & a_{12} & \cdots & a_{1n}\cr
\vdot...
...r}}\right]
= \left[{\matrix{d_1\cr \vdots\cr d_n\cr}}\right],
\end{displaymath}](c3_764.gif) |
(8) |
let
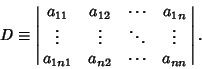 |
(9) |
If
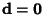 , then nondegenerate solutions exist only if
, then nondegenerate solutions exist only if 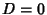 .
If
.
If
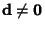 and
and 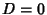 , the system has no unique solution. Otherwise, compute
, the system has no unique solution. Otherwise, compute
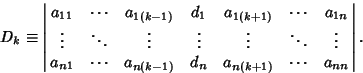 |
(10) |
Then 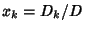 for
for
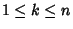 . In the 3-D case, the Vector analog of Cramer's rule is
. In the 3-D case, the Vector analog of Cramer's rule is
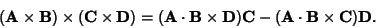 |
(11) |
See also Determinant, Linear Algebra, Matrix, System of Equations, Vector
© 1996-9 Eric W. Weisstein
1999-05-25
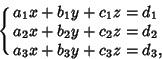
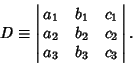
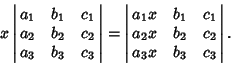
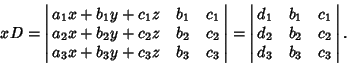
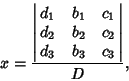

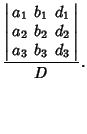
![]() equations so, given a system of
equations so, given a system of ![]() linear equations
linear equations
![\begin{displaymath}
\left[{\matrix{
a_{11} & a_{12} & \cdots & a_{1n}\cr
\vdot...
...r}}\right]
= \left[{\matrix{d_1\cr \vdots\cr d_n\cr}}\right],
\end{displaymath}](c3_764.gif)