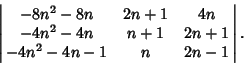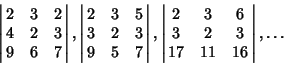Determinants are mathematical objects which are very useful in the analysis and solution of systems of linear equations. As
shown in Cramer's Rule, a nonhomogeneous system of linear equations has a nontrivial solution Iff the
determinant of the system's Matrix is Nonzero (so that the Matrix is nonsingular). A 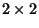 determinant is defined to be
determinant is defined to be
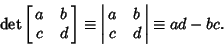 |
(1) |
A 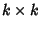 determinant can be expanded by Minors to obtain
determinant can be expanded by Minors to obtain
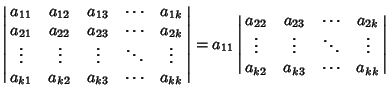
|
|
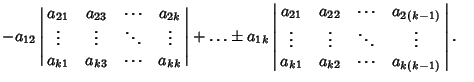
|
(2) |
A general determinant for a Matrix A has a value
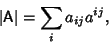 |
(3) |
with no implied summation over 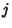 and where
and where 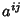 is the Cofactor of
is the Cofactor of 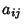 defined by
defined by
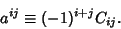 |
(4) |
Here, C is the
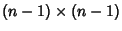 Matrix formed by eliminating row
Matrix formed by eliminating row 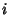 and column
and column 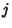 from A, i.e., by
Determinant Expansion by Minors.
from A, i.e., by
Determinant Expansion by Minors.
Given an 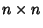 determinant, the additive inverse is
determinant, the additive inverse is
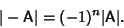 |
(5) |
Determinants are also Distributive, so
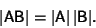 |
(6) |
This means that the determinant of a Matrix Inverse can be found as follows:
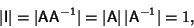 |
(7) |
where I is the Identity Matrix, so
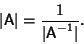 |
(8) |
Determinants are Multilinear in rows and columns, since
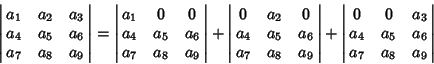 |
(9) |
and
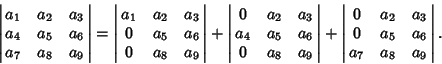 |
(10) |
The determinant of the Similarity Transformation of a matrix is equal to the determinant of the original
Matrix
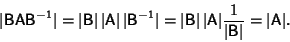 |
(11) |
The determinant of a similarity transformation minus a multiple of the unit Matrix is given by
The determinant of a Matrix Transpose equals the determinant of the original Matrix,
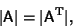 |
(13) |
and the determinant of a Complex Conjugate is equal to the Complex Conjugate of the determinant
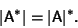 |
(14) |
Let 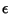 be a small number. Then
be a small number. Then
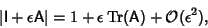 |
(15) |
where
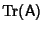 is the Trace of A. The determinant takes on a particularly simple form for a
Triangular Matrix
is the Trace of A. The determinant takes on a particularly simple form for a
Triangular Matrix
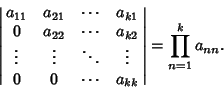 |
(16) |
Important properties of the determinant include the following.
- 1. Switching two rows or columns changes the sign.
- 2. Scalars can be factored out from rows and columns.
- 3. Multiples of rows and columns can be added together without changing the determinant's value.
- 4. Scalar multiplication of a row by a constant
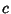 multiplies the determinant by
multiplies the determinant by 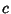 .
.
- 5. A determinant with a row or column of zeros has value 0.
- 6. Any determinant with two rows or columns equal has value 0.
Property 1 can be established by induction. For a 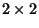 Matrix, the determinant is
Matrix, the determinant is
For a 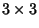 Matrix, the determinant is
Matrix, the determinant is
Property 2 follows likewise. For 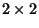 and
and 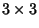 matrices,
matrices,
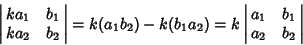 |
(19) |
and
 |
(20) |
Property 3 follows from the identity
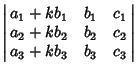
|
|
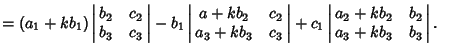
|
(21) |
If 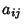 is an
is an 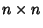 Matrix with
Matrix with 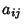 Real Numbers, then
Real Numbers, then
![$\mathop{\rm det}[a_{ij}]$](d1_683.gif) has the interpretation as the oriented
has the interpretation as the oriented 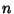 -dimensional Content of the Parallelepiped spanned
by the column vectors
-dimensional Content of the Parallelepiped spanned
by the column vectors ![$[a_{i,1}]$](d1_684.gif) , ...,
, ..., ![$[a_{i,n}]$](d1_685.gif) in
in 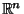 . Here, ``oriented'' means that, up to a change of
. Here, ``oriented'' means that, up to a change of 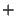 or
or
 Sign, the number is the
Sign, the number is the 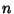 -dimensional Content, but the Sign depends on the ``orientation'' of
the column vectors involved. If they agree with the standard orientation, there is a
-dimensional Content, but the Sign depends on the ``orientation'' of
the column vectors involved. If they agree with the standard orientation, there is a 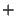 Sign; if not, there is a
Sign; if not, there is a
 Sign. The Parallelepiped spanned by the
Sign. The Parallelepiped spanned by the 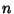 -D vectors
-D vectors 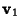 through
through 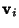 is the collection
of points
is the collection
of points
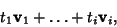 |
(22) |
where 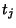 is a Real Number in the Closed Interval [0,1].
is a Real Number in the Closed Interval [0,1].
There are an infinite number of 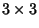 determinants with no 0 or
determinants with no 0 or 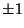 entries having unity determinant. One
parametric family is
entries having unity determinant. One
parametric family is
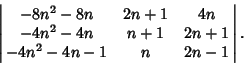 |
(23) |
Specific examples having small entries include
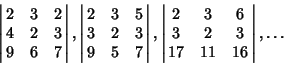 |
(24) |
(Guy 1989, 1994).
See also Circulant Determinant, Cofactor, Hessian Determinant, Hyperdeterminant, Immanant,
Jacobian, Knot Determinant, Matrix, Minor, Permanent, Vandermonde Determinant,
Wronskian
References
Arfken, G. ``Determinants.'' §4.1 in Mathematical Methods for Physicists, 3rd ed.
Orlando, FL: Academic Press, pp. 168-176, 1985.
Guy, R. K. ``Unsolved Problems Come of Age.'' Amer. Math. Monthly 96, 903-909, 1989.
Guy, R. K. ``A Determinant of Value One.'' §F28 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 265-266, 1994.
© 1996-9 Eric W. Weisstein
1999-05-24
![]() determinant is defined to be
determinant is defined to be
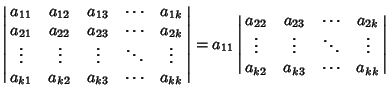
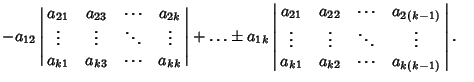
![]() determinant, the additive inverse is
determinant, the additive inverse is
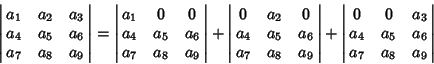
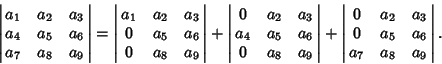
![]() be a small number. Then
be a small number. Then
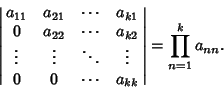
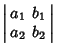
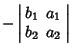
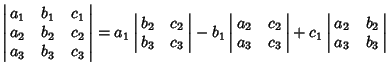
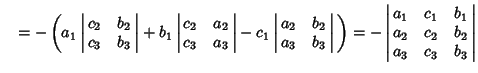
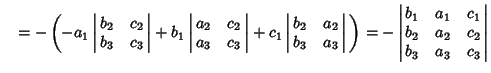
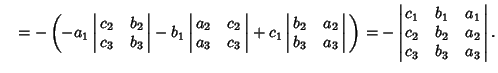

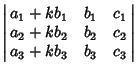
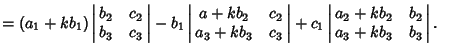
![]() is an
is an ![]() Matrix with
Matrix with ![]() Real Numbers, then
Real Numbers, then
![]() has the interpretation as the oriented
has the interpretation as the oriented ![]() -dimensional Content of the Parallelepiped spanned
by the column vectors
-dimensional Content of the Parallelepiped spanned
by the column vectors ![]() , ...,
, ..., ![]() in
in ![]() . Here, ``oriented'' means that, up to a change of
. Here, ``oriented'' means that, up to a change of ![]() or
or
![]() Sign, the number is the
Sign, the number is the ![]() -dimensional Content, but the Sign depends on the ``orientation'' of
the column vectors involved. If they agree with the standard orientation, there is a
-dimensional Content, but the Sign depends on the ``orientation'' of
the column vectors involved. If they agree with the standard orientation, there is a ![]() Sign; if not, there is a
Sign; if not, there is a
![]() Sign. The Parallelepiped spanned by the
Sign. The Parallelepiped spanned by the ![]() -D vectors
-D vectors ![]() through
through ![]() is the collection
of points
is the collection
of points
![]() determinants with no 0 or
determinants with no 0 or ![]() entries having unity determinant. One
parametric family is
entries having unity determinant. One
parametric family is