|
|
|
Also known as Laplacian Determinant Expansion by Minors. Let
![]() denote the Determinant of a
Matrix M, then
denote the Determinant of a
Matrix M, then
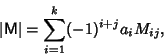
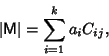
See also Cofactor, Determinant
References
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 169-170, 1985.