|
|
|
The trace of an ![]() Square Matrix A is defined by
Square Matrix A is defined by
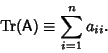 |
(1) |
| (2) | |||
| (3) | |||
| (4) |
| (5) |
| (6) |
| (7) |
The trace of a product of square matrices is independent of the order of the multiplication since
| (8) |
| (9) |
| (10) |
The value of the trace can be found using the fact that the matrix can always be transformed to a coordinate system where the
z-Axis lies along the axis of rotation. In the new coordinate system, the Matrix is
![\begin{displaymath}
{\hbox{\sf A}}' = \left[{\matrix{\cos \phi & \sin \phi & 0\cr -\sin \phi & \cos \phi & 0\cr 0 & 0 & 1\cr}}\right],
\end{displaymath}](t_1059.gif) |
(11) |
| (12) |
References
Lang, S. Linear Algebra, 3rd ed. New York: Springer-Verlag, pp. 40 and 64, 1987.
|
|
|
© 1996-9 Eric W. Weisstein