An antisymmetric matrix is a Matrix which satisfies the identity
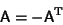 |
(1) |
where
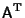 is the Matrix Transpose. In component notation, this becomes
is the Matrix Transpose. In component notation, this becomes
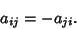 |
(2) |
Letting 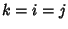 , the requirement becomes
, the requirement becomes
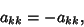 |
(3) |
so an antisymmetric matrix must have zeros on its diagonal. The general  antisymmetric matrix is of the form
antisymmetric matrix is of the form
![\begin{displaymath}
\left[{\matrix{
0 & a_{12} & a_{13}\cr
-a_{12} & 0 & a_{23}\cr
-a_{13} & -a_{23} & 0\cr}}\right].
\end{displaymath}](a_1094.gif) |
(4) |
Applying
 to both sides of the antisymmetry
condition gives
to both sides of the antisymmetry
condition gives
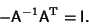 |
(5) |
Any Square Matrix can be expressed as the sum of symmetric and antisymmetric parts. Write
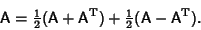 |
(6) |
But
![\begin{displaymath}
{\hbox{\sf A}}=\left[{\matrix{
a_{11} & a_{12} & \cdots & a...
...ots & \vdots\cr
a_{n1} & a_{n2} & \cdots & a_{nn}\cr}}\right]
\end{displaymath}](a_1098.gif) |
(7) |
![\begin{displaymath}
{\hbox{\sf A}}^{\rm T} =\left[{\matrix{
a_{11} & a_{21} & \...
...ts & \vdots\cr
a_{1n} & a_{2n} & \cdots & a_{nn}\cr}}\right],
\end{displaymath}](a_1099.gif) |
(8) |
so
![\begin{displaymath}
{\hbox{\sf A}}+{\hbox{\sf A}}^{\rm T}=\left[{\matrix{
2a_{1...
... a_{1n}+a_{n1} & a_{2n}+a_{n2} & \cdots & 2a_{nn}\cr}}\right],
\end{displaymath}](a_1100.gif) |
(9) |
which is symmetric, and
![\begin{displaymath}
{\hbox{\sf A}}-{\hbox{\sf A}}^{\rm T}=\left[{\matrix{ 0 & a_...
... -(a_{1n}-a_{n1}) & -(a_{2n}-a_{n2}) & \cdots & 0\cr}}\right],
\end{displaymath}](a_1101.gif) |
(10) |
which is antisymmetric.
See also Skew Symmetric Matrix, Symmetric Matrix
© 1996-9 Eric W. Weisstein
1999-05-25
![\begin{displaymath}
\left[{\matrix{
0 & a_{12} & a_{13}\cr
-a_{12} & 0 & a_{23}\cr
-a_{13} & -a_{23} & 0\cr}}\right].
\end{displaymath}](a_1094.gif)
![]() to both sides of the antisymmetry
condition gives
to both sides of the antisymmetry
condition gives
![\begin{displaymath}
{\hbox{\sf A}}=\left[{\matrix{
a_{11} & a_{12} & \cdots & a...
...ots & \vdots\cr
a_{n1} & a_{n2} & \cdots & a_{nn}\cr}}\right]
\end{displaymath}](a_1098.gif)
![\begin{displaymath}
{\hbox{\sf A}}^{\rm T} =\left[{\matrix{
a_{11} & a_{21} & \...
...ts & \vdots\cr
a_{1n} & a_{2n} & \cdots & a_{nn}\cr}}\right],
\end{displaymath}](a_1099.gif)
![\begin{displaymath}
{\hbox{\sf A}}+{\hbox{\sf A}}^{\rm T}=\left[{\matrix{
2a_{1...
... a_{1n}+a_{n1} & a_{2n}+a_{n2} & \cdots & 2a_{nn}\cr}}\right],
\end{displaymath}](a_1100.gif)
![\begin{displaymath}
{\hbox{\sf A}}-{\hbox{\sf A}}^{\rm T}=\left[{\matrix{ 0 & a_...
... -(a_{1n}-a_{n1}) & -(a_{2n}-a_{n2}) & \cdots & 0\cr}}\right],
\end{displaymath}](a_1101.gif)