A symmetric matrix is a Square Matrix which satisfies
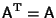 where
where
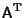 denotes the
Transpose, so
denotes the
Transpose, so
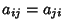 . This also implies
. This also implies
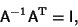 |
(1) |
where I is the Identity Matrix. Written explicitly,
![\begin{displaymath}
\left[{\matrix{
a_{11} & a_{12} & \cdots & a_{1n}\cr
a_{21...
...ts & \vdots\cr
a_{n1} & a_{n2} & \cdots & a_{nn}\cr}}\right].
\end{displaymath}](s3_1883.gif) |
(2) |
The symmetric part of any Matrix may be obtained from
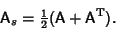 |
(3) |
A Matrix A is symmetric if it can be expressed in the form
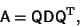 |
(4) |
where
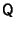 is an Orthogonal Matrix and
is an Orthogonal Matrix and
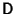 is a Diagonal Matrix. This is equivalent to the
Matrix equation
is a Diagonal Matrix. This is equivalent to the
Matrix equation
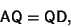 |
(5) |
which is equivalent to
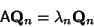 |
(6) |
for all 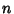 , where
, where
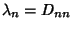 . Therefore, the diagonal elements of
. Therefore, the diagonal elements of
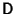 are the
Eigenvalues of
are the
Eigenvalues of
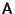 , and the columns of
, and the columns of
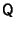 are the corresponding Eigenvectors.
are the corresponding Eigenvectors.
See also Antisymmetric Matrix, Skew Symmetric Matrix
References
Nash, J. C. ``Real Symmetric Matrices.''
Ch. 10 in Compact Numerical Methods for Computers: Linear Algebra
and Function Minimisation, 2nd ed. Bristol, England: Adam Hilger, pp. 119-134, 1990.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() where
where
![]() denotes the
Transpose, so
denotes the
Transpose, so
![]() . This also implies
. This also implies
![\begin{displaymath}
\left[{\matrix{
a_{11} & a_{12} & \cdots & a_{1n}\cr
a_{21...
...ts & \vdots\cr
a_{n1} & a_{n2} & \cdots & a_{nn}\cr}}\right].
\end{displaymath}](s3_1883.gif)