|
|
|
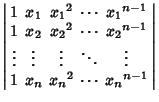 |
|||
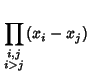 |
See also Vandermonde Matrix
References
Chapman, R. ``A Polynomial Taking Integer Values.'' Math. Mag. 69, 121, 1996.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA:
Academic Press, p. 1111, 1979.
Sharpe, D. §2.9 in Rings and Factorization. Cambridge, England: Cambridge University Press, 1987.