|
|
|
A procedure for decomposing an ![]() matrix
matrix
![]() into a product of a lower Triangular Matrix
into a product of a lower Triangular Matrix
![]() and an upper Triangular Matrix
and an upper Triangular Matrix
![]() ,
,
| (1) |
![\begin{displaymath}
\left[{\matrix{l_{11} & 0 & 0\cr l_{21} & l_{22} & 0\cr l_{3...
...{21} & a_{22} & a_{23}\cr a_{31} & a_{32} & a_{33}\cr}}\right]
\end{displaymath}](l2_1010.gif) |
(2) |
![\begin{displaymath}
\left[{\matrix{l_{11}u_{11} & l_{11}u_{12} & l_{11}u_{13}\cr...
...21} & a_{22} & a_{23}\cr a_{31} & a_{32} & a_{33}\cr}}\right].
\end{displaymath}](l2_1011.gif) |
(3) |
|
|
(4) |
|
|
(5) |
|
|
(6) |
| (7) |
| (8) | |||
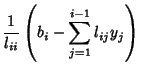 |
(9) |
| (10) | |||
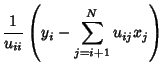 |
(11) |
See also Cholesky Decomposition, QR Decomposition, Triangular Matrix
References
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``LU Decomposition and Its Applications.''
§2.3 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 34-42, 1992.
|
|
|
© 1996-9 Eric W. Weisstein