|
|
|
If there is an Integer ![]() such that
such that
| (1) |
A list of quadratic residues for ![]() is given below (Sloane's A046071), with those numbers
is given below (Sloane's A046071), with those numbers ![]() not in the list being quadratic
nonresidues of
not in the list being quadratic
nonresidues of ![]() .
.
| Quadratic Residues | |
| 1 | (none) |
| 2 | 1 |
| 3 | 1 |
| 4 | 1 |
| 5 | 1, 4 |
| 6 | 1, 3, 4 |
| 7 | 1, 2, 4 |
| 8 | 1, 4 |
| 9 | 1, 4, 7 |
| 10 | 1, 4, 5, 6, 9 |
| 11 | 1, 3, 4, 5, 9 |
| 12 | 1, 4, 9 |
| 13 | 1, 3, 4, 9, 10, 12 |
| 14 | 1, 2, 4, 7, 8, 9, 11 |
| 15 | 1, 4, 6, 9, 10 |
| 16 | 1, 4, 9 |
| 17 | 1, 2, 4, 8, 9, 13, 15, 16 |
| 18 | 1, 4, 7, 9, 10, 13, 16 |
| 19 | 1, 4, 5, 6, 7, 9, 11, 16, 17 |
| 20 | 1, 4, 5, 9, 16 |
Given an Odd Prime ![]() and an Integer
and an Integer ![]() , then the Legendre Symbol is given by
, then the Legendre Symbol is given by
| (2) |
| (3) |
| (4) |
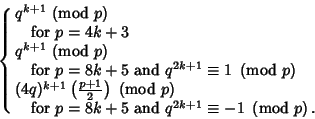 |
(5) |
More generally, let ![]() be a quadratic residue modulo an Odd Prime
be a quadratic residue modulo an Odd Prime ![]() . Choose
. Choose ![]() such that the Legendre Symbol
such that the Legendre Symbol
![]() . Then defining
. Then defining
| (6) | |||
| (7) | |||
| (8) |
| (9) | |||
| (10) |
| (11) |
The following table gives the Primes which have a given number ![]() as a quadratic residue.
as a quadratic residue.
| Primes | |
|
|
|
|
|
|
| 2 | |
| 3 | |
| 5 | |
| 6 |
Finding the Continued Fraction of a Square Root ![]() and using
the relationship
and using
the relationship
| (12) |
| (13) |
The number of Squares ![]() in
in ![]() is related to the number
is related to the number ![]() of quadratic
residues in
of quadratic
residues in ![]() by
by
| (14) |
See also Euler's Criterion, Multiplicative Function, Quadratic Reciprocity Theorem, Riemann Hypothesis
References
Burton, D. M. Elementary Number Theory, 4th ed. New York: McGraw-Hill, p. 201, 1997.
Courant, R. and Robbins, H. ``Quadratic Residues.'' §2.3 in Supplement to Ch. 1 in
What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford, England: Oxford University Press, pp. 38-40, 1996.
Guy, R. K. ``Quadratic Residues. Schur's Conjecture'' and ``Patterns of Quadratic Residues.'' §F5 and F6 in
Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 244-248, 1994.
Niven, I. and Zuckerman, H. An Introduction to the Theory of Numbers, 4th ed. New York: Wiley, p. 84, 1980.
Rosen, K. H. Ch. 9 in Elementary Number Theory and Its Applications, 3rd ed. Reading, MA: Addison-Wesley, 1993.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, pp. 63-66, 1993.
Sloane, N. J. A. Sequence
A046071
in ``The On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
Stangl, W. D. ``Counting Squares in
Wagon, S. ``Quadratic Residues.'' §9.2 in Mathematica in Action. New York: W. H. Freeman, pp. 292-296, 1991.
![]() .'' Math. Mag. 69, 285-289, 1996.
.'' Math. Mag. 69, 285-289, 1996.
|
|
|
© 1996-9 Eric W. Weisstein