|
|
|
First published in Riemann (1859), the Riemann hypothesis states that the
nontrivial Roots of the Riemann Zeta Function
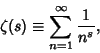 |
(1) |
In 1914, Hardy ![]() proved that an Infinite number of values for
proved that an Infinite number of values for ![]() can be found for which
can be found for which ![]() and
and
![]() . However, it is not known if all nontrivial roots
. However, it is not known if all nontrivial roots ![]() satisfy
satisfy ![]() , so the conjecture remains
open. André Weil proved the Riemann hypothesis to be true for field functions (Weil 1948, Eichler 1966, Ball and
Coxeter 1987). In 1974, Levin showed that at least 1/3 of the Roots must lie on the Critical Line
(Le Lionnais 1983), a result which has since been sharpened to 40% (Vardi 1991, p. 142). It is known that the zeros are
symmetrical placed about the line
, so the conjecture remains
open. André Weil proved the Riemann hypothesis to be true for field functions (Weil 1948, Eichler 1966, Ball and
Coxeter 1987). In 1974, Levin showed that at least 1/3 of the Roots must lie on the Critical Line
(Le Lionnais 1983), a result which has since been sharpened to 40% (Vardi 1991, p. 142). It is known that the zeros are
symmetrical placed about the line ![]() .
.
The Riemann hypothesis is equivalent to ![]() , where
, where ![]() is the de Bruijn-Newman Constant (Csordas
et al. 1994). It is also equivalent to the assertion that for some constant
is the de Bruijn-Newman Constant (Csordas
et al. 1994). It is also equivalent to the assertion that for some constant ![]() ,
,
| (2) |
The hypothesis was computationally tested and found to be true for the first ![]() zeros by Brent et al. (1982).
Brent's calculation covered zeros
zeros by Brent et al. (1982).
Brent's calculation covered zeros ![]() in the region
in the region
![]() .
.
There is also a finite analog of the Riemann hypothesis concerning the location of zeros for function fields defined by
equations such as
| (3) |
See also Critical Line, Extended Riemann Hypothesis, Gronwall's Theorem, Mertens Conjecture, Mills' Constant, Riemann Zeta Function
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 75, 1987.
Brent, R. P. ``On the Zeros of the Riemann Zeta Function in the Critical Strip.'' Math. Comput. 33, 1361-1372, 1979.
Brent, R. P.; van de Lune, J.; te Riele, H. J. J.; and Winter, D. T. ``On the Zeros of the Riemann Zeta
Function in the Critical Strip. II.'' Math. Comput. 39, 681-688, 1982.
Abstract available at ftp://nimbus.anu.edu.au/pub/Brent/rpb070a.dvi.Z.
Csordas, G.; Smith, W.; and Varga, R. S. ``Lehmer Pairs of Zeros, the de Bruijn-Newman Constant and the Riemann
Hypothesis.'' Constr. Approx. 10, 107-129, 1994.
Eichler, M. Introduction to the Theory of Algebraic Numbers and Functions. New York: Academic Press, 1966.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 25, 1983.
Odlyzko, A. ``The
Riemann, B. ``Über die Anzahl der Primzahlen unter einer gegebenen Grösse,'' Mon. Not. Berlin Akad., pp. 671-680, Nov. 1859.
Sloane, N. J. A. Sequence
A002410/M4924
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
van de Lune, J. and te Riele, H. J. J. ``On The Zeros of the Riemann Zeta-Function in the Critical Strip. III.''
Math. Comput. 41, 759-767, 1983.
van de Lune, J.; te Riele, H. J. J.; and Winter, D. T. ``On the Zeros of the Riemann Zeta Function in the Critical Strip. IV.''
Math. Comput. 46, 667-681, 1986.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, p. 33, 1991.
Weil, A. Sur les courbes algébriques et les variétès qui s'en déduisent. Paris, 1948.
![]() th Zero of the Riemann Zeta Function and 70 Million of Its Neighbors.''
th Zero of the Riemann Zeta Function and 70 Million of Its Neighbors.''
|
|
|
© 1996-9 Eric W. Weisstein