|
|
|
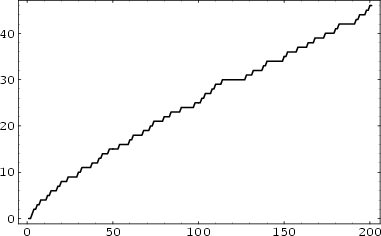
The function ![]() giving the number of Primes less than
giving the number of Primes less than ![]() (Shanks 1993, p. 15). The first few values are 0, 1, 2, 2,
3, 3, 4, 4, 4, 4, 5, 5, 6, 6, 6, ... (Sloane's A000720). The following table gives the values of
(Shanks 1993, p. 15). The first few values are 0, 1, 2, 2,
3, 3, 4, 4, 4, 4, 5, 5, 6, 6, 6, ... (Sloane's A000720). The following table gives the values of ![]() for powers of 10
(Sloane's A006880; Hardy and Wright 1979, p. 4; Shanks 1993, pp. 242-243; Ribenboim 1996, p. 237). Deleglise and Rivat (1996) have
computed
for powers of 10
(Sloane's A006880; Hardy and Wright 1979, p. 4; Shanks 1993, pp. 242-243; Ribenboim 1996, p. 237). Deleglise and Rivat (1996) have
computed ![]() .
.
| Method | Time | Storage |
| Legendre |
|
|
| Meissel |
|
|
| Lehmer |
|
|
| Mapes' |
|
|
| Lagarias-Miller-Odlyzko |
|
|
| Lagarias-Odlyzko 1 |
|
|
| Lagarias-Odlyzko 2 |
|
|
A modified version of the prime counting function is given by
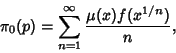
The notation ![]() is also used to denote the number of Primes of the form
is also used to denote the number of Primes of the form ![]() (Shanks 1993, pp. 21-22).
Groups of Equinumerous values of
(Shanks 1993, pp. 21-22).
Groups of Equinumerous values of ![]() include (
include (![]() ,
, ![]() ), (
), (![]() ,
, ![]() ),
(
),
(![]() ,
, ![]() ,
, ![]() ,
, ![]() ), (
), (![]() ,
, ![]() ),
(
),
(![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ),
(
),
(![]() ,
, ![]() ,
, ![]() ,
, ![]() ), (
), (![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ),
and so on. The values of
),
and so on. The values of ![]() for small
for small ![]() are given in the following table for the first few
powers of ten (Shanks 1993).
are given in the following table for the first few
powers of ten (Shanks 1993).
| 1 | 2 | 1 | 2 | |
| 11 | 13 | 11 | 13 | |
| 80 | 87 | 80 | 87 | |
| 611 | 617 | 609 | 619 | |
| 4784 | 4807 | 4783 | 4808 | |
| 39231 | 39266 | 39175 | 39322 | |
| 332194 | 332384 | 332180 | 332398 |
| 0 | 2 | 1 | 0 | |
| 5 | 7 | 7 | 5 | |
| 40 | 47 | 42 | 38 | |
| 306 | 309 | 310 | 303 | |
| 2387 | 2412 | 2402 | 2390 | |
| 19617 | 19622 | 19665 | 19593 | |
| 166104 | 166212 | 166230 | 166032 |
| 1 | 1 | |
| 11 | 12 | |
| 80 | 86 | |
| 611 | 616 | |
| 4784 | 4806 | |
| 39231 | 39265 |
| 0 | 1 | 1 | 0 | 1 | 0 | |
| 3 | 4 | 5 | 3 | 5 | 4 | |
| 28 | 27 | 30 | 26 | 29 | 27 | |
| 203 | 203 | 209 | 202 | 211 | 200 | |
| 1593 | 1584 | 1613 | 1601 | 1604 | 1596 | |
| 13063 | 13065 | 13105 | 13069 | 13105 | 13090 |
| 0 | 1 | 1 | 1 | |
| 5 | 7 | 6 | 6 | |
| 37 | 44 | 43 | 43 | |
| 295 | 311 | 314 | 308 | |
| 2384 | 2409 | 2399 | 2399 | |
| 19552 | 19653 | 19623 | 19669 | |
| 165976 | 166161 | 166204 | 166237 |
Note that since ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are Equinumerous,
are Equinumerous,
Erdös proved that there exist at least one Prime of the form ![]() and at least one Prime of the
form
and at least one Prime of the
form ![]() between
between ![]() and
and ![]() for all
for all ![]() .
.
The smallest ![]() such that
such that ![]() for
for ![]() , 3, ... are 2, 27, 96, 330, 1008, ... (Sloane's A038625), and the
corresponding
, 3, ... are 2, 27, 96, 330, 1008, ... (Sloane's A038625), and the
corresponding ![]() are 1, 9, 24, 66, 168, 437, ... (Sloane's A038626). The number of solutions of
are 1, 9, 24, 66, 168, 437, ... (Sloane's A038626). The number of solutions of ![]() for
for
![]() , 3, ... are 4, 3, 3, 6, 7, 6, ... (Sloane's A038627).
, 3, ... are 4, 3, 3, 6, 7, 6, ... (Sloane's A038627).
See also Bertelsen's Number, Equinumerous, Prime Arithmetic Progression, Prime Number Theorem, Riemann Weighted Prime-Power Counting Function
References
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, pp. 134-135, 1994.
Brent, R. P. ``Irregularities in the Distribution of Primes and Twin Primes.'' Math. Comput. 29, 43-56, 1975.
Deleglise, M. and Rivat, J. ``Computing
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/hrdyltl/hrdyltl.html
Forbes, T. ``Prime
Guiasu, S. ``Is There Any Regularity in the Distribution of Prime Numbers at the Beginning of the Sequence of
Positive Integers?'' Math. Mag. 68, 110-121, 1995.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.
Lagarias, J.; Miller, V. S.; and Odlyzko, A. ``Computing
Lagarias, J. and Odlyzko, A. ``Computing
Mapes, D. C. ``Fast Method for Computing the Number of Primes Less than a Given Limit.'' Math. Comput. 17, 179-185, 1963.
Meissel, E. D. F. ``Über die Bestimmung der Primzahlmenge innerhalb gegebener Grenzen.'' Math. Ann. 2, 636-642, 1870.
Ribenboim, P. The New Book of Prime Number Records, 3rd ed. New York: Springer-Verlag, 1996.
Riesel, H. ``The Number of Primes Below
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, 1993.
Sloane, N. J. A. Sequences
A038625,
A038626,
A038627,
A000720/M0256, and
A006880/M3608
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 74-76, 1991.
Wolf, M. ``Unexpected Regularities in the Distribution of Prime Numbers.'' http://rose.ift.uni.wroc.pl/~mwolf/.
![]() : The Meissel, Lehmer, Lagarias, Miller, Odlyzko Method.''
Math. Comput. 65, 235-245, 1996.
: The Meissel, Lehmer, Lagarias, Miller, Odlyzko Method.''
Math. Comput. 65, 235-245, 1996.
![]() -tuplets.'' http://www.ltkz.demon.co.uk/ktuplets.htm.
-tuplets.'' http://www.ltkz.demon.co.uk/ktuplets.htm.
![]() : The Meissel-Lehmer Method.'' Math. Comput. 44, 537-560, 1985.
: The Meissel-Lehmer Method.'' Math. Comput. 44, 537-560, 1985.
![]() : An Analytic Method.'' J. Algorithms 8, 173-191, 1987.
: An Analytic Method.'' J. Algorithms 8, 173-191, 1987.
![]() .'' Prime Numbers and Computer Methods for Factorization, 2nd ed.
Boston, MA: Birkhäuser, pp. 10-12, 1994.
.'' Prime Numbers and Computer Methods for Factorization, 2nd ed.
Boston, MA: Birkhäuser, pp. 10-12, 1994.
|
|
|
© 1996-9 Eric W. Weisstein