|
|
|
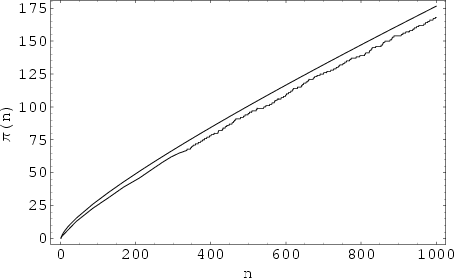
The theorem giving an asymptotic form for the Prime Counting Function ![]() for number of Primes less than
some Integer
for number of Primes less than
some Integer ![]() . Legendre
. Legendre ![]() (1808) suggested that, for large
(1808) suggested that, for large ![]() ,
,
| (1) |
| (2) |
| (3) |
For small ![]() , it has been checked and always found that
, it has been checked and always found that
![]() . However, Skewes proved that the first crossing of
. However, Skewes proved that the first crossing of
![]() occurs before
occurs before
![]() (the Skewes Number). The upper bound for the crossing has
subsequently been reduced to
(the Skewes Number). The upper bound for the crossing has
subsequently been reduced to ![]() . Littlewood (1914) proved that the Inequality reverses infinitely often for
sufficiently large
. Littlewood (1914) proved that the Inequality reverses infinitely often for
sufficiently large ![]() (Ball and Coxeter 1987). Lehman (1966) proved that at least
(Ball and Coxeter 1987). Lehman (1966) proved that at least ![]() reversals occur for numbers
with 1166 or 1167 Decimal Digits.
reversals occur for numbers
with 1166 or 1167 Decimal Digits.
Chebyshev (Rubinstein and Sarnak 1994) put limits on the Ratio
| (4) |
| (5) |
Hadamard and Vallée Poussin proved the prime number theorem by showing that the Riemann Zeta Function ![]() has
no zeros of the form
has
no zeros of the form ![]() (Smith 1994, p. 128). In particular, Vallée Poussin showed that
(Smith 1994, p. 128). In particular, Vallée Poussin showed that
| (6) |
Riemann ![]() estimated the Prime Counting Function with
estimated the Prime Counting Function with
| (7) |
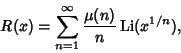 |
(8) |
The prime number theorem is equivalent to
| (9) |
The Riemann Hypothesis is equivalent to the assertion that
| (10) |
| (11) | |||
| (12) |
Ramanujan ![]() showed that for sufficiently large
showed that for sufficiently large ![]() ,
,
| (13) |
| (14) |
See also Bertrand's Postulate, Dirichlet's Theorem, Gram Series, Prime Counting Function, Riemann's Formula, Riemann Function, Riemann-Mangoldt Function, Riemann Weighted Prime-Power Counting Function, Skewes Number
References
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed.
New York: Dover, pp. 62-64, 1987.
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, 1994.
Courant, R. and Robbins, H. ``The Prime Number Theorem.'' §1.2c in Supplement to Ch. 1 in
What is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed.
Oxford, England: Oxford University Press, pp. 27-30, 1996.
Davenport, H. ``Prime Number Theorem.'' Ch. 18 in Multiplicative Number Theory, 2nd ed.
New York: Springer-Verlag, pp. 111-114, 1980.
de la Vallée Poussin, C.-J. ``Recherches analytiques la théorie des nombres premiers.'' Ann. Soc. scient. Bruxelles 20,
183-256, 1896.
Hadamard, J. ``Sur la distribution des zéros de la fonction
Hardy, G. H. and Wright, E. M. ``Statement of the Prime Number Theorem.'' §1.8 in
An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 9-10, 1979.
Ingham, A. E. The Distribution of Prime Numbers. London: Cambridge University Press, p. 83, 1932.
Legendre, A. M. Essai sur la Théorie des Nombres. Paris: Duprat, 1808.
Lehman, R. S. ``On the Difference
Littlewood, J. E. ``Sur les distribution des nombres premiers.'' C. R. Acad. Sci. Paris 158, 1869-1872, 1914.
Nagell, T. ``The Prime Number Theorem.'' Ch. 8 in Introduction to Number Theory. New York: Wiley, 1951.
Riemann, G. F. B. ``Über die Anzahl der Primzahlen unter einer gegebenen Grösse.''
Monatsber. Königl. Preuss. Akad. Wiss. Berlin, 671, 1859.
Rubinstein, M. and Sarnak, P. ``Chebyshev's Bias.'' Experimental Math. 3, 173-197, 1994.
Selberg, A. and Erdös, P. ``An Elementary Proof of the Prime Number Theorem.'' Ann. Math. 50, 305-313, 1949.
Shanks, D. ``The Prime Number Theorem.'' §1.6 in Solved and Unsolved Problems in Number Theory, 4th ed.
New York: Chelsea, pp. 15-17, 1993.
Smith, D. E. A Source Book in Mathematics. New York: Dover, 1994.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 25-35, 1991.
![]() et ses conséquences arithmétiques (').''
Bull. Soc. math. France 24, 199-220, 1896.
et ses conséquences arithmétiques (').''
Bull. Soc. math. France 24, 199-220, 1896.
![]() .'' Acta Arith. 11, 397-410, 1966.
.'' Acta Arith. 11, 397-410, 1966.
|
|
|
© 1996-9 Eric W. Weisstein